laetidom a écrit:Peut-être que le " donc" (je me le suis permis car on avait une puissance impaire et non paire)...
Le problème, à mon avis, il est là : est ce que tu crois que Julie (ou l'immense majorité des Lycéens) percute que, vu que la puissance est impaire, il n'y a pas de soucis est que la fonction puissance en question est bien injective (pour utiliser le mot qui fait peur...) ?
Perso, je pense pas et j'aurais tendance à penser que de ne pas signaler qu'il y a à cette endroit un problème mathématique profond (celui de l'injectivité de la fonction f qui permet de passer de f(x)=f(a) à x=a) c'est quand même assez ennuyeux.
Et surtout, c'est ennuyeux du fait que, bien avant le supérieur, ils auront à manipuler ce type de chose : dés le collège avec le x²=2² qui n'implique pas x=2, puis au Lycée avec par exemple cos(x)=cos(Pi/3) qui n'implique pas x=Pi/3.
Après, là où je sais pas quoi en penser, c'est que Julie affirme que
"je n'ai jamais vu en classe comment résoudre ce genre d'equation" alors que, vu que 864 n'est pas un cube parfait de toute façon on ne peut pas exprimer la solution de cette équation sans utiliser de racine cubique. Et qui dit utiliser des racines cubique, dit évidement qu'on les a étudié en cours, donc qu'on a parlé de la bijectivité de la fonction x->x^3, même si on a été obligé de l'exprimer je sais pas comment vu que le mot "bijectif" est, me semble-t-il, lui aussi passé à la poubelle.
Enfin, bref, Julie a forcément vu en cours que,
contrairement au cas des carrés, on a bien
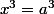
qui implique

. Par contre, je sais pas du tout comment on le démontre au Lycée (et je me demande au fond si je ne préfère pas... ne pas savoir...)
P.S. : A titre de culture, pour les cubes (et uniquement les cubes), on peut s'en sortir si on connait les équations du second degré (ou la forme canonique) : On vérifie (en développant le terme de droite) que
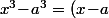(x^2\!+\!ax\!+\!a^2))
puis on calcule le discriminant (ou la forme canonique) du terme du second degré
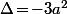
qui est strictement négatif si

est non nul donc le trinôme ne s'annule jamais.
L'unique solution pour que le produit soit nul est

.
?
? (u et y sont des nombres réels)

