Bonjour, mon sujet est :
Dans un repère orthonormé, on donne les points A (-2;3), B(0;1) et C (2;5).
On note Oméga (x;y) le centre circonscrit au triangle ABC.
On admet que O est le centre du cercle circonscrit au triangle ABC si et seulement si OA²= OB² = OC².
1)Écrire un système de deux équations à deux inconnues dont les coordonnées de O sont solutions.
2)Déduire les coordonnées du point O.
3) Calculer le rayon du cercle circonscrit au triangle ABC
1) J'ai calculé les longueurs en faisant :
IA²=IB² donc(xA-xI)²+(yA-yI)²=(xB-xI)²+(yB-yI)² équation 1
IA²=IC² donc(xA-xI)²+(yA-yI)²=(xC-xI)²+(yC-yI)² équation 2
I étant le point Omega
J'ai donc remplacé les lettres par chiffre et développé :
équation 1:(-2-xI)²+(3-yI)²=(0-xI)²+(1-yI)²
4-4xI+xI²+9-6yI+yI²=xI²+1-2yI+yI²
Equation 2 : (-2 -xI)² + (3-yI)² = (2 - xI)² + (5 -yI)²
4-4xI+xI²+9-6yI+yI²= 4- 4xI² + 25 -10yI²
Mais je suis bloqué ici en fait, quelqu'un peut me dire ce qu'il faut faire par la suite?
Equation dans un repére orthonormé niveau seconde
6 messages
- Page 1 sur 1
Salut !
Pourquoi appelé le centre du cercle circonscrit , puis
, puis  , puis
, puis  ?
?
Equation 1 : petite erreur :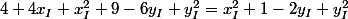 .
.
Equation 2 : tout est faux. Le membre de gauche, parce que tu l'avais déjà faux dans la précédente équation ; le membre de droite, parce que tu n'as pas développé correctement deux identités remarquables.
:+++:
Malex28 a écrit:Bonjour, mon sujet est :
Dans un repère orthonormé, on donne les points A (-2;3), B(0;1) et C (2;5).
On note Oméga (x;y) le centre circonscrit au triangle ABC.
On admet que O est le centre du cercle circonscrit au triangle ABC si et seulement si OA²= OB² = OC².
1)Écrire un système de deux équations à deux inconnues dont les coordonnées de O sont solutions.
2)Déduire les coordonnées du point O.
3) Calculer le rayon du cercle circonscrit au triangle ABC
1) J'ai calculé les longueurs en faisant :
IA²=IB² donc(xA-xI)²+(yA-yI)²=(xB-xI)²+(yB-yI)² équation 1
IA²=IC² donc(xA-xI)²+(yA-yI)²=(xC-xI)²+(yC-yI)² équation 2
I étant le point Omega
J'ai donc remplacé les lettres par chiffre et développé :
équation 1:(-2-xI)²+(3-yI)²=(0-xI)²+(1-yI)²
4-4xI+xI²+9-6yI+yI²=xI²+1-2yI+yI²
Equation 2 : (-2 -xI)² + (3-yI)² = (2 - xI)² + (5 -yI)²
4-4xI+xI²+9-6yI+yI²= 4- 4xI² + 25 -10yI²
Mais je suis bloqué ici en fait, quelqu'un peut me dire ce qu'il faut faire par la suite?
Pourquoi appelé le centre du cercle circonscrit
Equation 1 : petite erreur :
Equation 2 : tout est faux. Le membre de gauche, parce que tu l'avais déjà faux dans la précédente équation ; le membre de droite, parce que tu n'as pas développé correctement deux identités remarquables.
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Malex28 a écrit:D'accord, merci beaucoup ! Mais peux-tu me dire ce que je dois faire après ça ?
Résoudre le système associé à ses deux équations.
Les termes en x²,y² se neutraliseront sans problèmes.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Malex28 a écrit:Pour l'equation 1 je fais : 4-4x+9-6y=1-2y
-4x-4y=-12 équation 1
Non?
Tu as même mieux :
Et là deuxième équation ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
