Bonjour tout le monde, je suis en term S,
j'ai un DM à rendre pour la rentrée, et je bute à la première question...
" Résoudre dans R l'équation cos(x) = 0 "
Pourriez vous me donner une méthode ou m'expliquer ?
Merci
:)
Equation dans R de cos(x)=0
8 messages
- Page 1 sur 1
Regardes sur un cercle trigonométrique quand est-ce qu'un cosinus s'annule ?
On trouve le cosinus en projetant le point du cercle trigonométrique sur l'axe des x. Donc on voit que c'est nul pour x=pi/2 ou 3pi/2 (=-pi/2) et puis après on peut faire des tours complets en plus donc le résultat c'est avec
avec 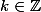
On trouve le cosinus en projetant le point du cercle trigonométrique sur l'axe des x. Donc on voit que c'est nul pour x=pi/2 ou 3pi/2 (=-pi/2) et puis après on peut faire des tours complets en plus donc le résultat c'est
+ ou - pi/2 et puis on peut ajouter des tours complets donc 2pi, ou 4pi, etc...
les angles sont toujours définis modulo 2pi, c'est à dire à un tour complet près.
On te demande de résoudre l'équation dans R, donc il faut donner toutes les valeurs, pas seulement celles qui sont comprises entre 0 et 2pi.
les angles sont toujours définis modulo 2pi, c'est à dire à un tour complet près.
On te demande de résoudre l'équation dans R, donc il faut donner toutes les valeurs, pas seulement celles qui sont comprises entre 0 et 2pi.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 215 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
