Bonjour !
J'ai un devoir de maths à rendre sur le produit scalaire.
Dans un exercice, on me demande de trouver une équation de cercle à partir de l'équation x2 + 2x + y2 - 6y + 5.
J'ai compris qu'il fallait la mettre les deux trinômes sous forme canonique, j'obtiens donc :
(x + 1)2 + (y - 3)2 = 13
Est ce juste? J'ai l'impression d'avoir manqué une étape?
De plus, la question suivante demandent les points d'intersections du cercle avec les axes de coordonnées du repère et je ne vois pas comment les trouver.
Merci de votre aide !
Équation de cercle
9 messages
- Page 1 sur 1
Re: Équation de cercle
Re-bonjour,
J'ai trouvé la réponse pour la question 2. (Celle avec les coordonnées des points d'intersection)
J'aimerais donc savoir si mon équation de départ est juste pour que je puisse continuer l'exercice sans partir avec une erreur ?
Merci beaucoup !
J'ai trouvé la réponse pour la question 2. (Celle avec les coordonnées des points d'intersection)
J'aimerais donc savoir si mon équation de départ est juste pour que je puisse continuer l'exercice sans partir avec une erreur ?
Merci beaucoup !
Re: Équation de cercle
Bonjour , non il y a une erreur
x²+2x = (x+1)²-1
y²-6y = (y-3)²-9
Remplace dans l'équation ....
Pour les points sur les axes, il faut résoudre un système en faisant intervenir les équations correspondantes
C'est à dire :
x=0 pour l'axe des ordonnées
y=0 pour celui des abscisses
Cela ramène à résoudre une équation du second degré, la première d'inconnue y, la seconde d'inconnue x.
x²+2x = (x+1)²-1
y²-6y = (y-3)²-9
Remplace dans l'équation ....
Pour les points sur les axes, il faut résoudre un système en faisant intervenir les équations correspondantes
C'est à dire :
x=0 pour l'axe des ordonnées
y=0 pour celui des abscisses
Cela ramène à résoudre une équation du second degré, la première d'inconnue y, la seconde d'inconnue x.
Re: Équation de cercle
Dans un exercice, on me demande de trouver une équation de cercle à partir de l'équation x2 + 2x + y2 - 6y + 5.
Ce n'est pas une équation !
Il s'agit sans doute de
qui correspond au cercle de centre
Re: Équation de cercle
C'est bien 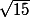
En résumé et pour stlblrax s'il lui arrivait de le lire
On peut obtenir le centre et le rayon du cercle d'équation de plusieurs manières
de plusieurs manières
a) La plus rapide (forme canonique des termes en x et en y) :
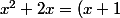^2-1)
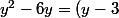^2-9)
^2+(y-3)^2-10 = 5)
^2 +(y-3)^2 = 15)
cercle de centre) et de rayon
et de rayon 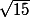
b) plus longue :
identification de cette équation à l'équation générale d'un cercle de centre (a ; b) et de rayon r
soit^2 +(y-b)^2 = r^2)

 par identification des termes en x
par identification des termes en x

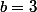 par identification des termes en y
par identification des termes en y

 par identification des termes constants
par identification des termes constants
En résumé et pour stlblrax s'il lui arrivait de le lire
On peut obtenir le centre et le rayon du cercle d'équation
a) La plus rapide (forme canonique des termes en x et en y) :
cercle de centre
b) plus longue :
identification de cette équation à l'équation générale d'un cercle de centre (a ; b) et de rayon r
soit
Re: Équation de cercle
Carpate, je ne cherche pas à avoir raison à tout prix mais dans l'énoncé de départ (certes incomplet puisque l'équation ne comporte pas le signe =) le nombre 5 est pour moi dans le membre de gauche et non pas dans celui de droite.
D'où 5 au lieu de 15.
D'où 5 au lieu de 15.
Re: Équation de cercle
C'est )à toi de mettre en forme les équation pour qu'elle soient de la forme
(x-a)²+(y-b²)=r² : équation dans le plan d'un cercle de rayon r et de cente (a;b)
x²+y²=1
est une équation dont la représentation graphique est le cercle de rayon 1 et de centre O
x²+y²-1=0
est la même équation écrite différemment et sa représentation graphiques est le cercle de rayon 1 et de centre O, pas un cercle de rayon 0.
(x+1)²+y²=4 est aussi un cercle de rayon 4
x²+2x+1+y²=4 est la même équation
x²+2x+y²=3 est la même équation, le3 à droite n'est pas le rayon du cercle car l'équation n'est pas sous la bonne forme.
L’exercice part de la 3ieme ligne pour remonter à le première
(x-a)²+(y-b²)=r² : équation dans le plan d'un cercle de rayon r et de cente (a;b)
x²+y²=1
est une équation dont la représentation graphique est le cercle de rayon 1 et de centre O
x²+y²-1=0
est la même équation écrite différemment et sa représentation graphiques est le cercle de rayon 1 et de centre O, pas un cercle de rayon 0.
(x+1)²+y²=4 est aussi un cercle de rayon 4
x²+2x+1+y²=4 est la même équation
x²+2x+y²=3 est la même équation, le3 à droite n'est pas le rayon du cercle car l'équation n'est pas sous la bonne forme.
L’exercice part de la 3ieme ligne pour remonter à le première
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
