TS - équation avec puissances

[Sulaheia]

Bonjour,

Dans un exercice, j'arrive à l'équation suivante :


n est un entier naturel non nul (ça limite déjà)

Du coup : 2n doit être un multiple de 5, j'essaye 5 pour n, hop ça marche (presque déçue ).
On peut aussi simplifier la fraction en enlevant 2 de chaque côté.

Mais est-ce qu'il y a une vraie méthode pour résoudre ce genre de trucs (une équation avec la variable en facteur et en puissance) ?

Merci

[zygomatique]

salut

la méthode est de retourner au collège pour y apprendre les règles de caclul sur les puissances et ses tables de multiplication :



...

[Lostounet]

Salut,

Je ne pense pas qu'il existe une méthode générale pour toutes les équations possibles et imaginables qui relient des puissances avec des facteurs. Mais dans des cas simples comme ici, on peut le faire manuellement:

n est un entier naturel non nul (ça limite déjà)

<=>


<=>


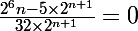
Or (***) implique comme tu l'as constaté, que n est multiple de 5 (lemme de Gauss) donc n = 5k (avec k naturel) ce qui signifie:







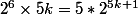
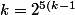Qui permet de constater que k = 1 convient (cela fait 2^0 et 1). Maintenant si k = 0 cela ne convient pas clairement. Il est clair aussi que si k >= 2, alors k < 2^(5(k - 1)) (par exemple par récurrence). Ou bien plus rapidement comme le fait Zygomatique, au choix.

(***) Cependant, il existe une fonction spéciale si tu veux, qui peut être utilisée pour des équations qui font intervenir du n en facteur et en puissance. C'est la fonction Oméga: https://fr.wikipedia.org/wiki/Fonction_W_de_Lambert

En l'occurrence, ici la fonction de Lambert (ou son prolongement analytique..) fournit deux solutions (réelles?) dont une est voisine de k ~ 0.035319 (donc n d'environ 0.1766... mais on se restreint à N donc elle n'a pas lieu !). L'autre est comme prévu k = 1

Mais elle est vraiment difficile à étudier (il te suffit de regarder sa ""courbe"" pour te rendre compte de sa complexité: elle semble associer à un même nombre.. plusieurs images!? mais en fait c'est pas tout à fait ça!). Donc on peut faire aussi une méthode numérique (niveau L1: méthode de Newton ou autre) pour s'épargner de telles horreurs.

[Sulaheia]

@Zygomatique
Et bim, c'était le tacle du lundi. J'espère que tu te sens mieux . Merci quand même pour ta réponse, je pense qu'en TS c'est effectivement ça qu'on attend (mais c'est dommage de ne pas savoir "vraiment" comment on fait).

@Lostounet
Merci d'avoir pris le temps d'expliquer tout ça. Je n'avais pas pensé à éliminer des cas (le 0 ou les autres par récurrence). Effectivement c'est ça qui me manquait.
Il faut vraiment que je me remette aux maths post bac, mais j'essaye de bien gérer le programme de lycée d'abord (et celui de collège ).

[Lostounet]

@Zygomatique
Et bim, c'était le tacle du lundi. J'espère que tu te sens mieux .

Bonjour,
C'est pas parce que c'est toi. C'est Zygo, il est toujours comme ça...
Mais on l'aime bien quand même :p

Et concernant le complément post-bac, celui-ci est disponible dès la L3 de maths pour pouvoir travailler avec de telles fonctions comme Oméga. Donc petit à petit..


Bonne journée

[zygomatique]

oui je suis comme ça ... mais ce n'est pas pour rien ... ni pour descendre quelqu'un ...

par contre descendre de niveau c'est simplement pour dire qu'avec des outils simples (ici de collège) mais qu'il faut bien maîtriser alors on peut résoudre des pb très pointus !!! avec un peu de réflexion ...

il est inutile d'aller chercher une quelconque fonction de Lambert ou autre outil très au-delà d'une réflexion élémentaire !!!

en particulier ici il est fondamental d'avoir en permanence en tête qu'on travaille dans les entiers ... et donc que des arguments de divisibilité suffisent amplement pour résoudre le pb

salut

la méthode est de retourner au collège pour y apprendre les règles de caclul sur les puissances et ses tables de multiplication :



...

les seuls diviseurs de 5 sont 1 et lui-même puisqu'il est premier ...

... et impair donc la seule puissance de 2 qui divise 5 est la puissance nulle

et on arrive au système qui a le bon gout d'être soluble (et pas que dans le pastis !!!) et donner la solution 5



PS : au passage tu as donc la méthode ... pour un fil posté dans le forum lycée ...