Equation assez spéciale ...

[upium666]

Bonjour à tous et à toutes !

Soit un réel x qui vérifie :



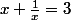
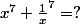
Je ne vois pas comment parvenir au résultat

Une aide ?

Merci !

[Cheche]

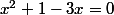
Cherches les solutions de cette équation et puis fait le calcul après.

[Sylviel]

Je ne suis pas vraiment d'accord avec Cheche. Ici je pense qu'il vaut mieux utiliser l'expression telle quelle. Tu connais x+1/x, comment faire pour avoir x^7+ 1/x^7 , quitte à avoir d'autres termes à gérer ?

[chan79]

Bonjour à tous et à toutes !

Soit un réel x qui vérifie :



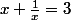
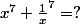
Je ne vois pas comment parvenir au résultat

Une aide ?

Merci !

calcule d'abord de deux façons:
pour obtenir
et continue de la même façon avec

puis

[Lostounet]

Bonjour à tous et à toutes !

Soit un réel x qui vérifie :



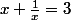
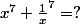
Je ne vois pas comment parvenir au résultat

Une aide ?

Merci !

Salut,

Une méthode amusante serait de remarquer que, pour tout n>=2
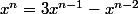
, puis de transformer l'expression au fur et à mesure (je ne sais pas si cela aboutit directement)...

Un autre exo sympa:

a,b et c trois réels vérifiant:
a + b + c = 0
a^2 + b^2 + c^2 = 74

Déterminer a^4 + b^4 + c^4

[Black Jack]

x²-3x+1=0

x = (3 +/- V5)/2

x² = (14 +/- 6V5)/4
x² = (7 +/- 3V5)/2
x^4 = (x²)²
x^4 = (49 + 45 +/- 42V5)/4
x^4 = (47 +/- 21V5)/2
x^6 = x^4*x²
x^6 = (47 +/- 21V5)/2 * (7 +/- 3V5)/2
x^6 = (47 +/- 21V5) * (7 +/- 3V5)/4
x^6 = (329 +/- 141V5 +/- 147V5 + 315)/4
x^6 = 161 +/- 72.V5
x^7 = x^6 * x
x^7 = (161 +/- 72.V5).(3 +/- V5)/2
x^7 = (483 +/- 161.V5 +/- 216.V5 + 360)/2
x^7 = (843 +/- 377.V5)/2

1/x^7 = 2/(843 +/- 377.V5)
1/x^7 = 2.(843 -/+ 377.V5)/[(843 +/- 377.V5).(843 -/+ 377.V5)]
1/x^7 = 2.(843 -/+ 377.V5)/(843² - 377²*5)
1/x^7 = (843 -/+ 377.V5)/2

x^7 + 1/(x^7) = (843 +/- 377.V5)/2 + (843 -/+ 377.V5)/2
x^7 + 1/(x^7) = 843

Pour voir la démo, sélectionner le texte avec la souris.


:zen:

[chan79]

Salut,



a,b et c trois réels vérifiant:
a + b + c = 0
a^2 + b^2 + c^2 = 74

Déterminer a^4 + b^4 + c^4

En élevant au carré (a²+b²+c²) ainsi que (a+b+c) on arrive au résultat

[Lostounet]

Comment .. ?

[Black Jack]

Comment .. ?

(a+b+c)² = 0

a² + b² + c² + 2(ab + ac + bc) = 0
V74 + 2(ab + ac + bc) = 0
2(ab + ac + bc) = -V74
4.(ab + ac + bc)² = 74
4(a²b²+a²c²+b²c² + 2(a²bc+ab²c+abc²)) = 74
a²b²+a²c²+b²c² = 37/2 - 2(a²bc+ab²c+abc²)
a²b²+a²c²+b²c² = 37/2 - 2abc(a+b+c)
a²b²+a²c²+b²c² = 37/2

*****

(a²+b²+c²) = V74
(a²+b²+c²)² = 74
a^4 + b^4 + c^4 + 2(a²b²+b²c²+a²c²) = 74
a^4 + b^4 + c^4 = 74 - 2(a²b²+b²c²+a²c²)
a^4 + b^4 + c^4 = 74 - 2 * 37/2
a^4 + b^4 + c^4 = 37

:zen:

[Lostounet]

J'aime beaucoup ton style torcheur lol ! :)
Un vrai bulldozer :p

[chan79]

(a+b+c)² = 0

a² + b² + c² + 2(ab + ac + bc) = 0
V74 + 2(ab + ac + bc) = 0
2(ab + ac + bc) = -V74
4.(ab + ac + bc)² = 74
4(a²b²+a²c²+b²c² + 2(a²bc+ab²c+abc²)) = 74
a²b²+a²c²+b²c² = 37/2 - 2(a²bc+ab²c+abc²)
a²b²+a²c²+b²c² = 37/2 - 2abc(a+b+c)
a²b²+a²c²+b²c² = 37/2

*****

(a²+b²+c²) = V74
(a²+b²+c²)² = 74
a^4 + b^4 + c^4 + 2(a²b²+b²c²+a²c²) = 74
a^4 + b^4 + c^4 = 74 - 2(a²b²+b²c²+a²c²)
a^4 + b^4 + c^4 = 74 - 2 * 37/2
a^4 + b^4 + c^4 = 37

:zen:

j'ai fait la même chose :zen:

[upium666]

Sympas ces exos !

Donc en fait il suffit de jouer avec les puissances, de faire des substitutions si on veut généraliser n'est-ce pas ?