Troisième exercice de Lou24
Exercice 3:
Soit a € R. On définit l'application fa : (x1, x2, x3) ———>(ax1+x2 + x3, -2x1 + x2 + x3, x1+ 3x2 – ax3)
a) Soit (So) le système linéaire fa(x1, x2, x3) = 0 avec a comme paramètre. Échelonner (So). Sous quelle condition le système (So) a-t-il une unique solution?
b) A-t-on fa est bijective pour tout a € R? Justifier.
c) Soit (y1, y2, y3) € R³ fixé. Soit (S) le système linéaire fa(x1, x2, x3) = (y1, y2, y3) avec quatre paramètres a, y1, y 2 et y3. Échelonner (S). (On pourra s'aider de la question a).) Montrer que (S) est compatible si et seulement si : a^2+ 5a + 6 différent de 0 ou 7y1 + (3a - 1)y2 + (-a - 2)Y3 = 0.
d) En déduire, sans justifier, toutes les valeurs de a pour lesquelles fa est bijective.
Pour tout les exercices €= appartient a
Endomorphisme bijectif (Lou24)
2 messages
- Page 1 sur 1
Re: endomorphisme bijectif (Lou24)
Bonsoir,
question a
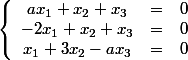
En calculant L1-L2 et -3L2+L3
x_1 &=& 0 \cr<br />7x_1-(3+a)x_3 &=& 0 \cr<br />-2x_1+x_2+x_3 &=& 0<br />\end{array}<br />\right.)
pour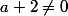 et
et 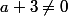 , on en déduit x_1=x_2=x_3=0
, on en déduit x_1=x_2=x_3=0
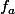 est donc injective (épimorphisme)
est donc injective (épimorphisme)
Le déterminant du système vaut:
(a+3))
question b
fa est bijective pour (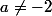 et
et )
question a
En calculant L1-L2 et -3L2+L3
pour
Le déterminant du système vaut:
question b
fa est bijective pour (
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
