Bonjour à toutes et à tous on m'a donné un exercice que je n'arrive pas à résoudre.
Je souhaite résoudre la double équation suivante
XY = 12
X ^2 + Y^2 = 25
si quelqu'un oeut m'aider à comprendre le rasionnement je lui en serait très reconnaissant.
Merci d'avance,
Double équation du 2e degré
9 messages
- Page 1 sur 1
Re: Double équation du 2e degré
Salut.
Piste :
a) Calculer (X+Y)² = ...
b) calculer (X-Y)² = ...
c) en déduire
(X+Y) = ...
(X-Y) = ...
d) Déterminer alors X et Y
Attention au point c, il y a une petite difficulté avec les signes.
Essaie.

Piste :
a) Calculer (X+Y)² = ...
b) calculer (X-Y)² = ...
c) en déduire
(X+Y) = ...
(X-Y) = ...
d) Déterminer alors X et Y
Attention au point c, il y a une petite difficulté avec les signes.
Essaie.
Re: Double équation du 2e degré
Bonsoir.
Pour trouver X et Y tels que :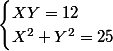 , on peut aussi, de façon plus naturelle, tirer de la première équation le fait que
, on peut aussi, de façon plus naturelle, tirer de la première équation le fait que 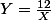 (car manifestement, X est non nul) et remplacer Y par cette expression dans la seconde équation, ce qui donne :
(car manifestement, X est non nul) et remplacer Y par cette expression dans la seconde équation, ce qui donne : 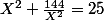 , soit
, soit 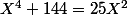 , ou encore
, ou encore 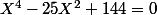 .
.
Cette dernière équation est dite bicarrée : on pose alors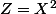 , et l'équation donne :
, et l'équation donne : 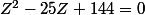 , que l'on peut résoudre à l'aide de son discriminant (49).
, que l'on peut résoudre à l'aide de son discriminant (49).
On trouve donc 2 valeurs de Z, donc deux valeurs de X². On en déduit ensuite les valeurs possibles pour X.
Pour trouver X et Y tels que :
Cette dernière équation est dite bicarrée : on pose alors
On trouve donc 2 valeurs de Z, donc deux valeurs de X². On en déduit ensuite les valeurs possibles pour X.
Cours particuliers par webcam : https://cours-maths-webcam.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
Re: Double équation du 2e degré
UnforgivenM a écrit:Bonjour à toutes et à tous on m'a donné un exercice que je n'arrive pas à résoudre.
Je souhaite résoudre la double équation suivante
XY = 12
X ^2 + Y^2 = 25
si quelqu'un oeut m'aider à comprendre le rasionnement je lui en serait très reconnaissant.
Merci d'avance,
Encore une couche:
(XY)^2=12^2=144 alors X^2*Y^2=144
Or deux nombres X^2 et Y^2 dont on connait la somme S=25 et le produit P=144 sont racines de l'équation:
Z^2-25Z+144=0.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Double équation du 2e degré
Lostounet a écrit:UnforgivenM a écrit:Bonjour à toutes et à tous on m'a donné un exercice que je n'arrive pas à résoudre.
Je souhaite résoudre la double équation suivante
XY = 12
X ^2 + Y^2 = 25
si quelqu'un oeut m'aider à comprendre le rasionnement je lui en serait très reconnaissant.
Merci d'avance,
Encore une couche:
(XY)^2=12^2=144 alors X^2*Y^2=144
Or deux nombres X^2 et Y^2 dont on connait la somme S=25 et le produit P=144 sont racines de l'équation:
Z^2-25Z+144=0.
Le problème est que ce résultat (concernant la somme et le produit de deux nombres) n'est plus au programme depuis longtemps au lycée (mais heureusement, il revient l'an prochain avec les nouveaux programmes). C'est la raison pour laquelle je me suis permis d'expliquer autrement.
Cours particuliers par webcam : https://cours-maths-webcam.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
Re: Double équation du 2e degré
@evaristeG
j'ai regardé un peu le site mathweb, la présentation est agréable, j'ai bien aimé la page sur l'origine des mots mathématiques :
https://www.mathweb.fr/euclide/201:8/09 ... /#more-801
j'ai regardé un peu le site mathweb, la présentation est agréable, j'ai bien aimé la page sur l'origine des mots mathématiques :
https://www.mathweb.fr/euclide/201:8/09 ... /#more-801
Re: Double équation du 2e degré
Merci. J'essaie de faire de mon mieux 
Cours particuliers par webcam : https://cours-maths-webcam.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
LaTeX, Maths & Python : https://www.mathweb.fr/
Re: Double équation du 2e degré
XY = 12
X ^2 + Y^2 = 25
géométriquement est la recherche de l'intersection de l'hyperbole y=12/x et du cercle de centre O et de rayon 5
Il y a intersection si (√12;√12) est à l'intérieur du cercle ( il y est de peu, le point est à environ 4.9 de O).
il y a alors 4 intersections.
X ^2 + Y^2 = 25
géométriquement est la recherche de l'intersection de l'hyperbole y=12/x et du cercle de centre O et de rayon 5
Il y a intersection si (√12;√12) est à l'intérieur du cercle ( il y est de peu, le point est à environ 4.9 de O).
il y a alors 4 intersections.
Re: Double équation du 2e degré
Bsr
Qui ne connait pas la formule connue de Pythagore
3²+4²=5² solution évidente
Qui ne connait pas la formule connue de Pythagore
3²+4²=5² solution évidente
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
