Bonsoir,
Ça fait déjà un petit moment que je coince sur plusieurs questions d'un exercice en particulier... La consigne étant : "Déterminer les valeurs des paramètres pour lequelles la division est exacte. Déterminé le quotient."
Une des questions est :
(x3 + 4x2 + ax + b) : (x2 + x + 1)
Mon problème, c'est que la métode que j'applique généralement utilise les solutions de l'équation x2+x+1 pour pouvoir annuler la première équation (je sais c'est pas clair, même pour moi en lisant je ne me comprends pas) je vais vous donner un exemple : (4x4+7x3-ax2+bx+24) : (x-2)(x+4) le "x" est bien sûr une lettre non une multiplication
Et là j'applique :
P(x) est divisible par (x-2) -> P(2) =0 donc 64+56-4a+2b+24=0
On laisse ça de côté...
De même P(x) est divisible par (x+4) -> P(-4)=0 donc 1024-448-16a-4b+24=0
Et là on a deux équations à deux inconnues, on les résouts et on arrive à : a=37 b=2
Puis après on reprend notre division du début en remplaçant a et b par ces nombres-ci, et on trouve le cotient !
Bref tout ça pour dire, dans mon cas de base, comment je fait si je ne peux pas factorisé le diviseur ...? Le mettre dans un style (x-5)(x+3) ...?
Car sinon comment je pourrais trouver "a" et "b" ?
Merci de votre lecture (j'espère ne pas vous avoir embrouillé)
Et j'attend avec impatience une réponse
Merci!
Division de polynômes avec des paramètres "a" et "b"
3 messages
- Page 1 sur 1
Re: Division de polynômes avec des paramètres "a" et "b"
Salut,
A mon sens, il y a (au moins) trois méthodes :
- Si tu as vu les nombre complexes, ben tu cherche la factorisation dans C de x²+x+1 et tu procède ensuite exactement comme dans l'exemple que tu donne.
- Sinon, tu écrit la division euclidienne de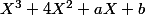 par
par 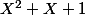 :
:
(X^2+X+1)+R(X)\ \ \ (*))
Comme on doit avoir<d^o(X^2\!+\!X\!+\!1)\!=\!2) , c'est que
, c'est que \!=\! \alpha X\!+\!\beta) .
.
Comme) multiplié par
multiplié par  ne doit produire que des termes de
ne doit produire que des termes de 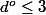 , c'est que
, c'est que \!=\!\gamma X\!+\!\delta)
Partant de ça, il n'y a plus qu'à développer et réduire le terme de droite de (*) puis à identifier les coefficients obtenus avec ceux de gauche pour en déduire la valeur de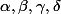 (en fonction de
(en fonction de  et
et  évidement).
évidement).
Et il n'y aura plus qu'à regarder à quelle(s) condition(s) sur et
et  on va avoir
on va avoir =0) , c'est à dire
, c'est à dire 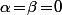 .
.
- Tu peut aussi faire exactement la même chose que çi dessus, mais en partant dés le départ de=0) .
.
Dans ce cas là, tu va directement chercher les valeurs qu'il faut prendre pour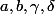 de façon à égaliser les deux expression à droite et à gauche du = dans (*).
de façon à égaliser les deux expression à droite et à gauche du = dans (*).
A mon sens, il y a (au moins) trois méthodes :
- Si tu as vu les nombre complexes, ben tu cherche la factorisation dans C de x²+x+1 et tu procède ensuite exactement comme dans l'exemple que tu donne.
- Sinon, tu écrit la division euclidienne de
Comme on doit avoir
Comme
Partant de ça, il n'y a plus qu'à développer et réduire le terme de droite de (*) puis à identifier les coefficients obtenus avec ceux de gauche pour en déduire la valeur de
Et il n'y aura plus qu'à regarder à quelle(s) condition(s) sur
- Tu peut aussi faire exactement la même chose que çi dessus, mais en partant dés le départ de
Dans ce cas là, tu va directement chercher les valeurs qu'il faut prendre pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 114 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
