Distance avec angles et distances

par **Coquard** » 09 Déc 2015, 14:05

Bonjour, je suis bloqué à l'exercice suivant :

"On ne peut pas mesurer directement la distance au sol de l'arbre A à la maison M du fait de la présence d'obstacles.
Les mesures de différentes distances et d'angles donnent les résultats indiqués sur ce schéma.
Calculer la distance AM."

Une solution ?

PS : L'image étant énorme, dézoomer !

par **Ben314** » 09 Déc 2015, 16:06

Salut,
Quand tu projette (orthogonalement) d'une droite sur une autre, y'a un truc qui s'appelle le "rapport de projection" et qui vaut ??? (en fonction de l'angle entre les deux droites)
Tu applique ça pour trouver la longueur des projetés sur la droite (AM) de tout les petits morceaux.

par **chan79** » 09 Déc 2015, 17:44

Une petite remarque:
Si on fait la figure en commençant par [AP] puis Q, R et M en respectant les angles et les distances, on constate que

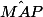
a bien l'air de mesurer 45° mais il faut l'établir.

par **Lostounet** » 09 Déc 2015, 18:04

Bonjour
P, Q, M ont-ils une raison d'être alignés?

Je vois pas l'obstacle qui leur aurait empêché la mesure directe de AM

par **Coquard** » 09 Déc 2015, 18:57

Ben314 a écrit:Salut,
Quand tu projette (orthogonalement) d'une droite sur une autre, y'a un truc qui s'appelle le "rapport de projection" et qui vaut ??? (en fonction de l'angle entre les deux droites)
Tu applique ça pour trouver la longueur des projetés sur la droite (AM) de tout les petits morceaux.

Je n'ai pas le niveau qui requiert ces connaissances...
Lostounet, les points ne sont pas alignés....

Mon prof m'a parlé d'angles droits : Les points S,T,U sur [AM], ASP, ATQ et AUR des angles droits 90°.

Mais je ne vois toujours pas !

par **chan79** » 09 Déc 2015, 19:30

On peut montrer que (AP) et (RM) sont perpendiculaires. Si elles se coupent en I, on peut montrer que AIM est isocèle. On a donc bien les 45° en A et on peut calculer AM.

par **laetidom** » 09 Déc 2015, 19:40

Coquard a écrit:Je n'ai pas le niveau qui requiert ces connaissances...
Lostounet, les points ne sont pas alignés....

Mon prof m'a parlé d'angles droits : Les points S,T,U sur [AM], ASP, ATQ et AUR des angles droits 90°.

Mais je ne vois toujours pas !

Bonsoir,

Je viens de calculer AM par la méthode de Ben, c'est facile (il faut savoir calculer un sinus ou un cosinus bien sûr), et je trouve AM =

+ 3 (

8.623982082 m

par **chan79** » 09 Déc 2015, 19:47

laetidom a écrit:Bonsoir,

Je viens de calculer AM par la méthode de Ben, c'est facile (il faut savoir calculer un sinus ou un cosinus bien sûr), et je trouve AM = + 3 ( 8.623982082 m

oui, en valeur exacte:

par **laetidom** » 09 Déc 2015, 19:49

chan79 a écrit:oui, en valeur exacte:

ah très bien, merci chan ! mais je n'ai pas réussi à trouver le

, peux-tu me briefer ?....

====> pas la peine, je viens de trouver :

3(sin75° + sin15°) :

sin75°=sin(45+30)=sin45cos30+sin30cos45 =

sin15° = sin(45-30)=sin45cos30-sin30cos45 =

donc

3(sin75° + sin15°) = 3(

+

) =

Bonne soirée.

par **Coquard** » 09 Déc 2015, 22:01

chan79 a écrit:On peut montrer que (AP) et (RM) sont perpendiculaires. Si elles se coupent en I, on peut montrer que AIM est isocèle. On a donc bien les 45° en A et on peut calculer AM.

Avec quelle méthode ?

par **Ben314** » 09 Déc 2015, 23:13

Quand on fait les bases de la trigo. au collège, on voit plus la notion de "rapport de projection" ?

par **chan79** » 10 Déc 2015, 10:28

Ben314 a écrit:Quand on fait les bases de la trigo. au collège, on voit plus la notion de "rapport de projection" ?

A vérifier, mais je crois qu'on ne parle que de cosinus d'un angle dans un triangle rectangle (en 4°)
Sinon, ici, on peut faire la figure en commençant par [AP] puis Q, R et M en respectant les angles et les distances sans utiliser l'angle de 45°.
On peut montrer que si (AP) et (RM) se coupent en I, AIM est rectangle isocèle, ce qui confirme l'angle de 45°. On obtient AM en multipliant AI par

.

par **Coquard** » 10 Déc 2015, 11:07

chan79 a écrit:A vérifier, mais je crois qu'on ne parle que de cosinus d'un angle dans un triangle rectangle (en 4°)
Sinon, ici, on peut faire la figure en commençant par [AP] puis Q, R et M en respectant les angles et les distances sans utiliser l'angle de 45°.
On peut montrer que si (AP) et (RM) se coupent en I, AIM est rectangle isocèle, ce qui confirme l'angle de 45°. On obtient AM en multipliant AI par .

Comment monter que (AP) et (RM) se coupent en I ?

par **chan79** » 10 Déc 2015, 12:56

Coquard a écrit:Comment monter que (AP) et (RM) se coupent en I ?

Avec les angles, on vérifie qu'elles ne sont pas parallèles et on nomme I leur point d'intersection.

par **Coquard** » 10 Déc 2015, 18:10

Je comprends rien... :cry:

Vous pouvez réexpliquer simplement ?

par **chan79** » 10 Déc 2015, 20:29

Coquard a écrit:Je comprends rien...

Vous pouvez réexpliquer simplement ?

vois la figure

par **Coquard** » 10 Déc 2015, 20:46

Je vois pas...

par **laetidom** » 10 Déc 2015, 22:00

Coquard a écrit:Je vois pas...

Bonsoir,

J'essaye chan de te "suppléer" (sourire),

@ Coquard,

En suivant sur la figure de chan :
triangle PQR : isocèle,

= 90° donc

=

= 45°, PR par Pythagore =

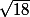
donc dans le triangle PIR :

= 180 - 60 -45 = 75° et

= 180 - 120 - 45 = 15°
donc

= 90°

IA = 2 +

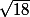
cos 15° =

IM = 5 +

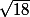
cos 75° =

Donc AM =

=

8.62398 m

par **Coquard** » 10 Déc 2015, 22:32

Justement, j'ai du mal avec ma figure car je n'ai pas de triangle apparent comme dans celle de chan79... :doh:

par **laetidom** » 11 Déc 2015, 10:38

Coquard a écrit:Justement, j'ai du mal avec ma figure car je n'ai pas de triangle apparent comme dans celle de chan79... :doh:

Bonjour,

Pourtant la figure que tu nous a joint et celle de chan, c'est la même !? non ?.....

...et mon explication découle des éléments de ta figure, à savoir le calcul des angles en R et P découle des angles présents dans la figure de départ !?......comment t'aider dans ce cas ....?

Distance avec angles et distances

Distance avec angles et distances

Qui est en ligne