La différence entre condition nécessaire et suffisante

[YasserKabiri]

Bonjour svp expliquez moi cela :
je ne peux pas faire la différence entre la condtion nécessaire et la condition suffisante. Quand dit-on que P est une condition suffisante ou nécessaire meme chose pour Q quand on a une implication P==>Q (P et Q deux assertions).

[hdci]

Bonjour,

Pour que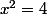 , il suffit que 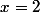et cela s'écrit



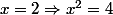
Mais ce n'est pas nécessaire car il y a d'autres nombres qui vérifient l'équation : ainsi, . Donc il n'est pas nécessaire que 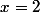pour avoir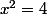

A contrario, pour que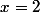 il est nécessaire que 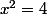(si 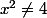, aucune chance que x soit égal à 2)

En synthèse dans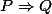 , on peut lire :

• Si P est vraie alors Q est nécessairement vraie : Q est donc une condition nécessaire pour P
• Pour avoir Q, il suffit que P soit vraie, mais ce n'est pas nécessaire : si P est fausse on ne sait rien dire de Q. Donc P est une condition suffisante pour Q.

[beagle]

Ma préférence plutôt que vrai faux est avoir ou ne pas avoir

Si P alors Q devient:
si j'ai P alors j'ai Q
La question est souvent oui, mais zalors, si j'ai Q j'ai P ?
Ben on n'en sait rien, si j'ai Q j'ai P ou bien je n'ai pas P.
Donc avoir Q n'est pas suffisant pour savoir si j'ai P
Q est non suffisant (sauf si équivalence, mais généralement et jusqu' à preuve du contraire)

Si je n'ai pas Q, je vais avoir P ou non?
avoir P c'est avoir Q, donc non
pour avoir P il m'est nécessaire d'avoir Q, Q est nécessaire

L'autre support un peu différent de celui de hdci *pour stabiliser tout cela est par exemple:
k entier,
si k multiple de 6 alors k est pair

* je ne vais pas tout embrouiller mais les ET les OU ne sont pas au meme endroit dans les deux exemples,
il me semble, vu de loin ...

[mathelot]

Bonjour,
Soient P et Q des propositions (avec valeur de vérité)
Supposons l'implication vraie :
Si P alors Q.

P est une condition suffisante pour Q
Q est une condition nécessaire pour P

[lyceen95]

Si tu veux devenir champion du monde de foot, il faut que tu t'inscrives dans un club de foot, c'est une condition nécessaire. Si tu ne fais pas cette première étape, tu es sur que tu ne seras jamais champion de foot.

Mais ce n'est pas une condition suffisante. Si tu t'inscris dans un club de foot, ça ne te garantis pas de devenir champion du monde.

C'est une condition nécessaire mais pas suffisante.

En langage un peu plus mathématique :
Proposition P : Je m'inscris dans un club de foot
Proposition Q : Je deviens champion du monde.
P est une condition nécessaire pour Q mais pas suffisante.

Si pas P, alors pas Q.

[beagle]

Une petite vision ensembliste?

si k multiple de 6, alors k multiple de 2

multiple de 6 = multiple de 2 et multiple de 3
multiple de 6 est l'intersection des multiples de 2 et de 3

si dans intersection multiple de 2 et multiple de 3 alors je suis dans les multiples de 2
Et etre dans les multiples de 2 c'est nécessaire mais pas suffisant.(pour etre dans multiple de 6)
Pour etre dans A inter B il est nécessaire d'ètre dans A, mais cela ne suffit pas,
il faut etre dans A qui est B aussi

L'eexemple de hdci est avec du ou
Si x=2 alors x²=4
x² =4 c'est : x=2 ou x=-2
etre x=2 ou -2 est nécessaire pour ètre =+2, mais cela ne suffit pas, il faut ne pas etre -2
x²=4 est nécessaire non suffisant.
ètre dans le A union B est nécessaire, mais cela ne suffit pas, il faut en plus ne pas ètre dans B

[Vassillia]

Bonjour à tous,

Je pense que la réponse a la question a été suffisamment détaillée mais pour faire plaisir à Beagle, on peut effectivement "voir" l'implication comme une inclusion avec :
"et" pour l'intersection
"ou" pour l'union .

On a toujours :
autrement dit (A et B) => A c'est à dire A est une condition nécessaire pour (A et B)
autrement dit A => (A ou B) c'est à dire A est une condition suffisante pour (A ou B)

[beagle]

Tien un fil de discussion sur l'implication qui ne dégènère pas.
Il n'est pas trop tard?

A implique B est la meme chose que
si A alors B
et c'est un connecteur logique
pas un conditionnel.
Euh mais que signifie une condition (nécessaire ou suffisante) sans conditionnel ?

[GaBuZoMeu]

Euh mais que signifie une condition (nécessaire ou suffisante) sans conditionnel ?

Bah, où est le problème ? On suppose avoir démontré
.
Dans ce cas : est une condition suffisante pour , et est une condition nécessaire pour.
Mais ces appellations ne font sens que parce qu'on a démontré l'énoncé ci-dessus, qui est la quantification universelle du prédicat , formé à partir des prédicats et au moyen du connecteur .

On a évoqué plus haut des opérations ensemblistes sur des parties et d'un univers . Les connecteurs logiques correspondent effectivement à des opérations ensemblistes :
: l'intersection, la plus grande partie de contenue à la fois dans et dans .
: la réunion, la plus petite partie de qui contient à la fois et .
: la plus grande partie de dont l'intersection avec est contenue dans .

Mais cette discussion technique nous emmène loin de la question basique de YasserKabiri.

[beagle]

Ok , merci GBZM,
cela nous emmène loin en effet.

Donc il n' y a pas de vrai problème.
Le "problème" pour moi est de dire comme le fait CC, il n' y a que deux si A alors B,
le langage commun
le langage mathématique qui est celui du scientifique.
Il me semble que la distance qui va au "cela nous emmène loin", oblige à considérer plusieurs si A alors B,
plutôt que 2 dans le parcours mathématique (et cc fait l'impasse sur la pédagogie et la construction du si a alors B au long des études,
tout comme dans le langage commun où il n' ya pas que des erreurs d'implication equivalence.

Car on peut discuter le fait que le commun des mortels ne soit pas logique dans ses raisonnements, comme si seul les logiciens pouvaient avoir le droit de vote bientôt, vu que les autres font n'importe quoi.
Vous auriez pu un peu discuter et chatouiller CC sur son analyse de la logique chez Plenel et Zemmour.
On a le sentiment que cela mène à un certain mépris du peuple son truc…
Cela va loin en effet….

[GaBuZoMeu]

Beagle, s'il te plaît, essaie de ne pas virer dans le n'importe quoi.

J'ai essayé de t'expliquer qu'il y a une différence entre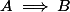 (une formule) et 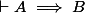(un théorème), ce dernier étant la même chose que .
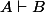J'ai essayé de t'expliquer que "condition nécessaire, condition suffisante" s'emploie dans le contexte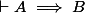 ou .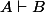

Prenons un exemple pour enfoncer le clou de la différence entre écrire une formule et énoncer un théorème.
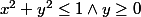est une formule dont l'extension dans 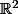est une partie du plan.
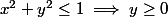est aussi une formule dont l'extension dans 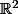est la réunion de l'extérieur du disque unité et du demi-plan supérieur fermé ; ici bien sûr, il serait malvenu de parler de condition nécessaire ou de condition suffisante. Ce n'est pas un théorème qui dirait que le disque unité fermé est contenu dans le demi-plan supérieur fermé.
Par contre, une fois qu'on a le théorème , on peut bien dire que 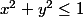est une condition suffisante pour 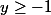. La nature du 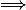n'a pourtant pas changé entre les deux situations.

Alors, pour aller dans ton sens, on pourrait dire que tu pointes une différence entre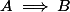 (une formule) et 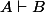(un théorème : sous l'hypothèse on a ).

[beagle]

Merci GBZM, dans la ref que j'avais mise où Barthélémy parlait des deux symboles, tu avais envoyé ce texte à la poubelle des sans intérèt.

Bon , donc moi je vois deux symboles mathématiques,
alors que j'ai toujours un seul si A alors B pour le moment.
ça c'est le premier point.

Le deuxième point serait de m'expliquer dans quel cadre un scientifique utilise un connecteur logique sans faire de causalité.
Par exemple:
Si la bactérie Klebsiella est habituellement sensible à la gentamycine, alors l'hémophilie est une maladie génétique de transmission récessive liée à l'X .
https://www.youtube.com/watch?v=tcngxS9m6K8
Tu as des exemples d'une utilisation qui ne serait pas aussi ridicule?

[GaBuZoMeu]

Le deuxième point serait de m'expliquer dans quel cadre un scientifique utilise un connecteur logique sans faire de causalité ?

Veux-tu que je te ramène à l'exercice "S'il y a une voyelle d'un côté de la carte, il y a un nombre pair de l'autre côté" ? Nulle causalité là-dedans. C'est pour cela que je trouve cet exercice instructif.
Aucune causalité dans le connecteur en logique.
Par exemple, en logique classique est équivalent à . Est-ce la cause et l'effet ou bien est-ce la cause et l'effet ?

Quand un scientifique étudie l'hypothèse d'une relation de cause à effet entre deux phénomènes, ça n'a pas grand chose à voir avec "utiliser un connecteur logique". On utilise un connecteur logique pour fabriquer un prédicat à partir de deux prédicats.

[beagle]

Ben l'exo des cartes deux faces nombre et lettre, on aurait pu connaitre le caractère instructif, si cela n'avait pas été un tu sais le faire ou pas, si tu ne réponds pas c'est que tu sais pas , nanani nananère.

Cet exo se résout avec l'utilisation de la logique prébac du si j'ai A alors j'ai B.
Et causalité ou pas, abus de langage ou pas
le si j'ai A alors j'ai B
il dit que j'ai B parce que j'ai A (ou quand j'aurais A, ou si je l'avais).
Donc c'est quelque part à cause d'avoir A que je sais que j'ai B.

S'agissant du si A alors B des scientifiques,
je ne vois toujours pas qu'il s'agisse d'autre chose que de la notion mathématique prébac,
si j'ai A alors j'ai B
Si on avait A alors on aurait du avoir B.

[GaBuZoMeu]

Bravo Beagle, tu apportes vraiment la lumière par ton discours clair et limpide !

[beagle]

On attend toujours l'utilisation d'un des deux signes maths, de l'unique si A alors B
pour résoudre l'exo lettre-nombre.
Je ne nie pas la pédagogie de l'exo puisque l'on a toujours rien derrière.
Fais le et tu verras la pédagogie.
J' ai pas vu.

bon ben allons - y prenons une lettre …

En causalité, je dis que je sais B PARCE QUE je sais A, ...

[GaBuZoMeu]

Je te signale que j'ai proposé cet exercice classique (et pas seulement sur le forum, mais aussi pour des étudiants ou un public lycéen). On peut donc penser que je l'ai fait, et que j'en ai éprouvé les vertus pédagogiques sur le fonctionnement de l'implication.

Je pense que tout a été dit, et que ce n'était d'ailleurs pas l'endroit, dans ce fil de lycéen, pour faire ça. Je sors.

[beagle]

Ben je ne nie absolument pas sa vertu pédagogique,
j'ai dit je ne la vois pas.

Je ne la vois pas au sens de changer mon utilisation du si A vrai alors B.

Peut-être qu'elle a des vertus pour ne pas passer par un stade primaire de si A vrai alors B.
Cela restera mystérieux.

Je reste, sinon on va dire qu'on sort ensemble.

[azf]

Je reste, sinon on va dire qu'on sort ensemble.

sinon on va dire qu'on est sur meetic.com ...bon ok je sort

[Vassillia]

Arf, je vais le faire cet exercice et tu vas voir Beagle que c'est un support visuel pedagogique comme tu aimes.
On veut vérifier la phrase "S'il y a une voyelle d'un côté de la carte, il y a un nombre pair de l'autre côté", quelles sont les cartes à retourner ?

- Si je vois une voyelle, il faut retourner la carte pour vérifier qu'il y a un nombre pair derriere
- Si je vois une consonne, il peut y avoir n'importe quoi derriere donc pas besoin de retourner
- Si je vois un nombre pair, il peut y avoir une voyelle derriere mais ce n'est pas obligé donc pas besoin de retourner
- Si je vois un nombre impair, attention si de l'autre coté il y a une voyelle, la phrase est fausse donc il faut retourner la carte pour vérifier qu'il n'y a pas de voyelle derriere.

Quel est l'interet ?
Pour que la phrase soit vraie, il n'y a pas besoin de vérifier ni consonne ni nombre pair.
Donc l'implication est vraie lorsqu'on a une consonne ou un nombre pair : V=>P se traduit par (non V) ou P
Il n'y a aucune causalité dans cette implication, c'est juste une phrase qui peut être vrai ou fausse en fonction des circonstances.

PS : Si tu veux mon avis, personne ne voulait vérifier que tu sais faire l'exercice, tout le monde s'en fiche.
Par contre initialement, certains (dont moi) espéraient avoir une discussion constructive, mais ce ne fut pas possible car tu veux imposer ton idée qu'un élève ne peut pas comprendre certaines notions. Je te rassure, ils peuvent comprendre quand ils se donnent la peine d'écouter.