Devoir maison sur exponentielle

par **Bertrand Hamant** » 01 Fév 2006, 13:55

bonjour j'ai un devoir maison à faire pour demain sur les expo.

soit f(x) = (1-2x)e^2x

calculer f' f'' et f''' c bon

Démontrer par récurrence que f^n(x) = 2^n(1-n-2x)e^2x

un peu bloqué

3) soit Mn de coordonnés (0 ;1) avec (xn ; yn) vérifier que les points Mn appartiennent à la courbe T d'équation = (e^2x)/4^x

en effet c la tangente

Démontre que la suite est xn est arithmétique

soit xn = x0 + nr = -2n et yn = (2)^n

lim de xn -00 et lim yn +00 est ce correcte merci de me répondre

par **tigri** » 01 Fév 2006, 13:59

bonjour

nous espérons voir tes recherches afin de te donner notre avis
Courage!!

par **Bertrand Hamant** » 01 Fév 2006, 14:05

en fait je trouve une limite de - 00 pour la suite xn et une limite de +00 pour yn. pour leur expression je trouve xn = x0 + -2n et yn = yo(2)^n

par **tigri** » 01 Fév 2006, 15:07

pour la récurrence:
vérifie que la formule espérée est vérifiée pour n=1 (avec ton f'(x) trouvé)
ensuite pose ton hypothèse de récurrence au rang K
puis démontre que la formule est encore vraie au rang k+1

par **allomomo** » 01 Fév 2006, 15:08

Salut,

1 -
Dérivée d'ordre 01 :

Dérivée d'ordre 02 :

2 - Démonstration par récurrence :

*

donc la propriété est vraie pour

* Soit

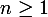
, supposons que :

alors :

* La proriété est vraie pour n=1 et hériditaire donc vraie pour tout entier naturel n supérieur ou égal à 1

par **Bertrand Hamant** » 01 Fév 2006, 15:48

et les limites sont bonnes ?

par **Bertrand Hamant** » 01 Fév 2006, 17:21

qu'en pensez vous ?

par **Bertrand Hamant** » 01 Fév 2006, 18:34

vous pensez que les limites sont bonnes pour les suites ?

par **Bertrand Hamant** » 01 Fév 2006, 18:55

est ce quelqu'un pourrait juste confirmer si les limites sont bonnes ou pas ?

par **fonfon** » 01 Fév 2006, 19:02

Salut, je pense qu'elles sont bonnes mais qu'est-ce que tu trouves pour xo et yo

par **Bertrand Hamant** » 01 Fév 2006, 19:15

merci de m'avoir répondu je commençais à désespèrer.

Parfois, la vie est tellement dure qu'on serait capable de tout abandonner, mais pourquoi tant de tristesses ?

merci encore de vos réponses

par **tigri** » 01 Fév 2006, 19:27

personnellement je n'ai pas compris le libellé de la question 3):
"soit Mn(0,1) avec (xn, yn) "
donc je ne pouvais pas te répondre, mais n'ai pas pu te le dire plus tôt

"la vie est parfois dure " c'est vrai, mais garde confiance

par **Bertrand Hamant** » 01 Fév 2006, 19:31

c'est difficile de garder confiance, quand tu te compares en sachant qu'au fond je suis pas mal

Devoir maison sur exponentielle

Devoir maison sur exponentielle

Qui est en ligne