Devoir Maison STMG

[Zakr0z]

Bonjour je travaille depuis peu sur un devoir Maison de Maths sur les Suites

Mais malheuresement je suis bloquer sur un exercice...Malgrés mes essais je n'arrive pas à trouver le sens de variation de la suite :

Soit la suite (Vn) définies pour tous entiers naturels n par:

Uo = -2

Un+1 = Un/3

Si vous pouvez m'aider je vous serais très reconnaissant

Bonne journée

[Beta]

Bonjour,

Il y a les classiques. Vous pouvez calculer et comparé le résultat par rapport à 1 ou regarder et le comparé par rapport à 0.

A vous de choisir la meilleur option

[aymanemaysae]

Bonjour ;

Tu peux aussi remarquer que la suite en question est une suite géométrique de raison q = 1/3
et de premier terme u_0 = - 2 ; donc pour tout n € IN , u_n = u_0 x q^n .

Ensuite tu peux utiliser les indications de Beta .

[Zakr0z]

Je vous remercie de votre aide ...
Malheureusement en utilisant la technique Un+1 - Un je ne retrouve pas de résultat conforme à l'exerce, l'erreur vient surement de ma part, j'ai effectué :
Un+1 = -2/3 Un+1-Un = -2/3 - 2 ----> pour Un = U0 Mais je ne suis pas sur de prendre un bon exemple
Seriez vous me dire le calcule pour parvenir au sens de variation de la suite ?

En vous remerciant
Cordialement

[Beta]

Si on souhaite procédé par 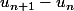, le plus simple est de remarqué, comme la dit aymanemaysae, que est une suite géométrique. Alors la première question est quel valeur de peut- on trouver avec cette déduction (aymanemaysae la décrite de manière général) ?

[Zakr0z]

Beta seriez vous me dire que signifie q^n que aymanemaysae à préciser pour parvenir au résultat de Un en fonction de U0

[Beta]

q est la raison. Par exemple, si alors 14 est la raison

[aymanemaysae]

q^n veut dire .

[Zakr0z]

Un+1 = q^n/3 ?
Que vaut q s'il vous plait

[Zakr0z]

Est-ce que la réponse est -2,6 ? donc la suite serait Décroissante ?

[Beta]

Si on a alors q est la raison.

Autrement dit, si s'exprime comme un multiple de lui même alors ce multiple est la raison. Or, ce multiples peut-être un réelle.

[Beta]

"Par lui même", je souhaitais plutôt dire "par son terme précédent"

[Beta]

Par exemple,

alors 3 est la raison

alors est la raison

[Zakr0z]

Merci! J'ai trouver 0 est-ce bon ?

[aymanemaysae]

Bonsoir ;


Tout d'abord tu dois revoir ton cours sur les suites et plus précisément sur les suites géométriques.

Rappel .

Soit dont le premier terme est et tel que pour tout avec .
Cette suite est une suite géométrique de premier terme et de raison .
Pour tout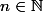 , et la somme des n premiers termes de cette suite est : .

Si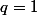 la suite est une suite constante dont tous les termes sont égaux à .
Si est une suite dont tous les termes sont nuls , sauf u_0 qui peut-être non nul .
Si la suite est une suite alternée dont tous les termes sont égaux soit à soit à .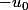


Dans ton exercice , tu as pour tou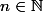t , et ;
donc tu as une suite géométrique de premier terme et de raison .

Maintenant tu as pour tout .

Ensuite , tu dois calculer : , et enfin tu remplaces par sa valeur déjà trouvée .

Conclusion : est-elle strictement positive , strictement négative ou nulle ?