Bonsoir
Quel est la méthode pour déterminer l'équation d'une courbe à partir d'un graphique.
A bientôt
Déterminer graphiquement l'équation d'une courbe
3 messages
- Page 1 sur 1
Re: Déterminer graphiquement l'équation d'une courbe
Pour avoir directement l'équation de la courbe, c'est impossible à moins d'avoir des informations en plus. On peut par contre s'en approcher, si on se place sur un segment  et qu'on veut approximer
et qu'on veut approximer  sur ce segment, on peut interpoler la fonction ou bien la décomposer en série de Fourier. Pour le premier cas, soit
sur ce segment, on peut interpoler la fonction ou bien la décomposer en série de Fourier. Pour le premier cas, soit  tels que l'on connaisse les valeurs de
tels que l'on connaisse les valeurs de ,\ldots,f(x_n)) (on peut les connaître graphiquement modulo l'imprécision de la mesure). Soit
(on peut les connaître graphiquement modulo l'imprécision de la mesure). Soit 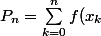L_k^{(n)}}) où
où }(x)=\prod_{1\leqslant i\neq k \leqslant n}\frac{x-x_i}{x_k-x_i}) appelé polynôme interpolateur de Lagrange. Alors
appelé polynôme interpolateur de Lagrange. Alors}(x_j)=1) si
si 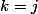 et
et  sinon de sorte que
sinon de sorte que =f(x_j)) pour tout
pour tout  , plus on prend de points (donc plus
, plus on prend de points (donc plus  est grand), plus
est grand), plus  va être une bonne approximation de
va être une bonne approximation de  . Dans le même esprit, si on pose
. Dans le même esprit, si on pose =\sum_{k=0}^n \binom{n}{k}f\left(a+k\frac{b-a}{n}\right)x^k(1-x)^{n-k}) appelé polynôme de Bernstein, plus
appelé polynôme de Bernstein, plus  est grand, plus
est grand, plus  est une bonne approximation de
est une bonne approximation de  . Concernant les séries de Fourier, si on pose
. Concernant les séries de Fourier, si on pose 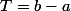 et
et =a_0+\sum_{k=1}^n{a_k\cos\left(\frac{2\pi k x}{T}\right)+b_k\sin\left(\frac{2\pi k x}{T}\right)) avec
avec 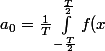dx) ,
, 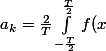\cos\left(\frac{2\pi k x}{T}\right)dx) et
et 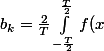\sin\left(\frac{2\pi k x}{T}\right)dx) pour tout
pour tout 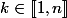 alors de même
alors de même  est une bonne approximation de
est une bonne approximation de  , plus
, plus  est grand, plus cette approximation est meilleure.
est grand, plus cette approximation est meilleure.
Re: Déterminer graphiquement l'équation d'une courbe
Niveau Lycée, c'est sans doute pas la réponse la plus simple.
Suivant l'allure, on peut regarder si elle ressemble à une des fonctions de référence.
ensuite 2 méthodes :
-> on choisi quelques points, juste ce qu'il faut pour poser un système.
-> on fait une méthode approchante avec l'aide des proba (régression)
Suivant l'allure, on peut regarder si elle ressemble à une des fonctions de référence.
ensuite 2 méthodes :
-> on choisi quelques points, juste ce qu'il faut pour poser un système.
-> on fait une méthode approchante avec l'aide des proba (régression)
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
