On considère une circonférence de rayon R qui coupe au moins un des axes de coordonnées. Soient A et B les intersections d'un axe de coordonnées avec cette circonférence.
- Détermine le lieu des centres des circonférences telles que OA . OB = R^2
- Analyse ce lieu
- Dessine les différents éléments et le lieu, avec R = 4 cm
(OA et OB sont des vecteurs)
Quelqu'un peut-il me dire comment aborder l'exercice ?
Détermine le lieu des centres des circonférences
8 messages
- Page 1 sur 1
Re: Détermine le lieu des centres des circonférences
Bonjour,
C'est quoi "O" ?
L'origine du repère ou autre chose ?
C'est quoi "O" ?
L'origine du repère ou autre chose ?
Re: Détermine le lieu des centres des circonférences
Black Jack a écrit:Bonjour,
C'est quoi "O" ?
L'origine du repère ou autre chose ?
Bonjour,
Désolé, ce n'est pas décrit précisément dans la donnée.
O est l'origine du repère orthonormé OXY, donc le point O(0;0).
Re: Détermine le lieu des centres des circonférences
Bonjour,
Equation des cercles de centre C(a;b) et de rayon R : (x-a)² + (y-b)² = R²
Cherchons les points de rencontre de ces cercles avec par exemple l'axe des ordonnées... d'équation x = 0
Il faut donc résoudre le système :
(x-a)² + (y-b)² = R²
x = 0
... donne les points de rencontre A et B cherchés : A(0 ; b + V(R²-a²)) et B(0 ; b - V(R²-a²))
avec V pour racine carrée.
vect(OA).vect(OB) = (b + V(R²-a²)) * (b - V(R²-a²))
vect(OA).vect(OB) = b² - R² + a² = a² + b² - R²
Et si on veut que vect(OA).vect(OB) = R², il faut donc que : a² + b² = 2R²
Les centres des circonférences appartiennent don à un cercle centre sur et de rayon V2 * R
... sous la contrainte qu'il faut que a <= R
Donc le lieu des centres des cercles qui coupent l'axe des ordonnées en 2 points A et B tel que vect(OA).vect(OB) sont 2 portions de cercle centré sur l'origine du repère, de rayon V2 * R et limité aux abscisses comprises dans [-a ; a]
****
On doit refaire un exercice similaire pour les cercles coupant l'axe des abscisses en 2 points ...
On devrait trouver que :
Le lieu des centres des cercles qui coupent l'axe des abscisses en 2 points A et B tel que vect(OA).vect(OB) sont 2 portions de cercle centré sur l'origine du repère, de rayon V2 * R et limité aux ordonnées comprises dans [-b ; b]
****
En regroupant les 2 lieux des centres des cercles ci dessus, le lieu des centres des cercles est le cercle complet de rayon V2.R centré sur l'origine du repère
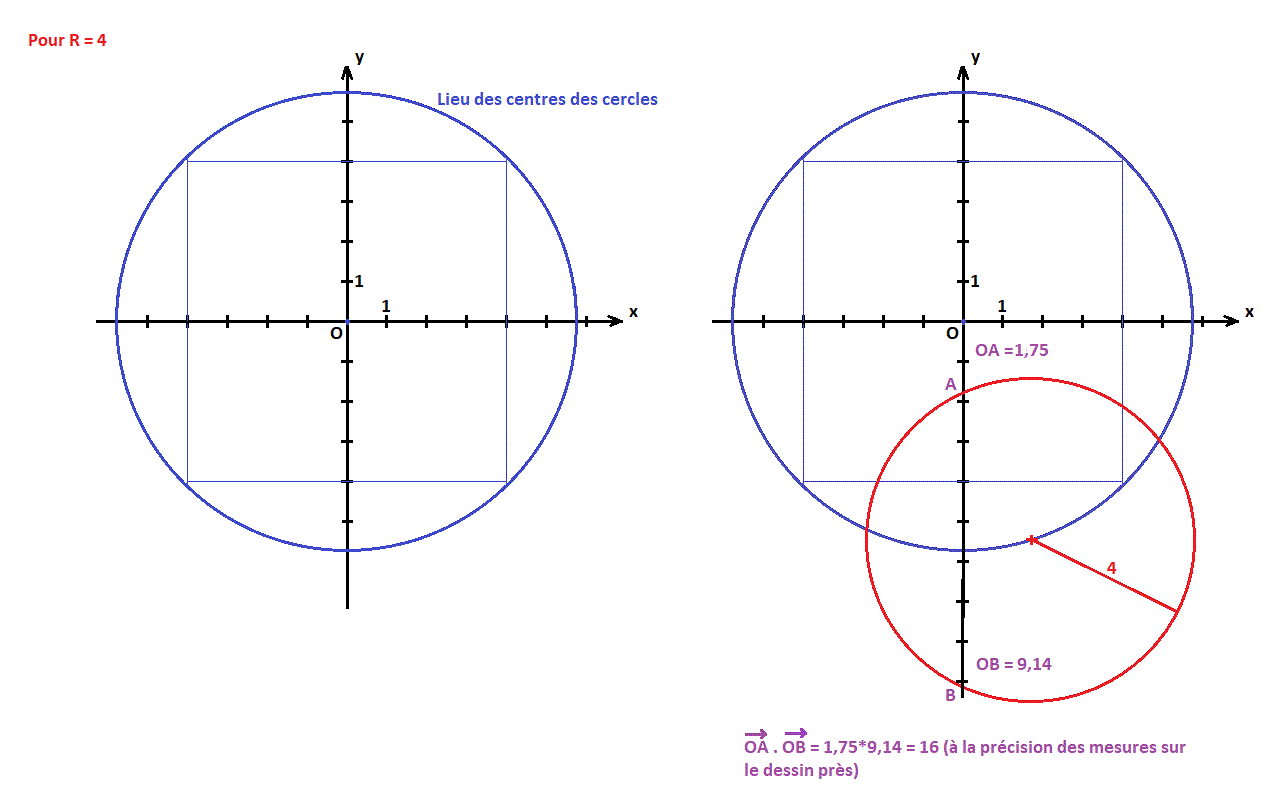
Sur le dessin de gauche, la représentation du lieu des centres des cercles de rayon 4 répondant à l'énoncé.
Sur le dessin de droite, la construction d'un des cercles de rayon 4 avec son centre appartenant au lieu cherché sur le dessin de gauche.

Equation des cercles de centre C(a;b) et de rayon R : (x-a)² + (y-b)² = R²
Cherchons les points de rencontre de ces cercles avec par exemple l'axe des ordonnées... d'équation x = 0
Il faut donc résoudre le système :
(x-a)² + (y-b)² = R²
x = 0
... donne les points de rencontre A et B cherchés : A(0 ; b + V(R²-a²)) et B(0 ; b - V(R²-a²))
avec V pour racine carrée.
vect(OA).vect(OB) = (b + V(R²-a²)) * (b - V(R²-a²))
vect(OA).vect(OB) = b² - R² + a² = a² + b² - R²
Et si on veut que vect(OA).vect(OB) = R², il faut donc que : a² + b² = 2R²
Les centres des circonférences appartiennent don à un cercle centre sur et de rayon V2 * R
... sous la contrainte qu'il faut que a <= R
Donc le lieu des centres des cercles qui coupent l'axe des ordonnées en 2 points A et B tel que vect(OA).vect(OB) sont 2 portions de cercle centré sur l'origine du repère, de rayon V2 * R et limité aux abscisses comprises dans [-a ; a]
****
On doit refaire un exercice similaire pour les cercles coupant l'axe des abscisses en 2 points ...
On devrait trouver que :
Le lieu des centres des cercles qui coupent l'axe des abscisses en 2 points A et B tel que vect(OA).vect(OB) sont 2 portions de cercle centré sur l'origine du repère, de rayon V2 * R et limité aux ordonnées comprises dans [-b ; b]
****
En regroupant les 2 lieux des centres des cercles ci dessus, le lieu des centres des cercles est le cercle complet de rayon V2.R centré sur l'origine du repère
Sur le dessin de gauche, la représentation du lieu des centres des cercles de rayon 4 répondant à l'énoncé.
Sur le dessin de droite, la construction d'un des cercles de rayon 4 avec son centre appartenant au lieu cherché sur le dessin de gauche.

Re: Détermine le lieu des centres des circonférences
Bonjour
On pouvait aussi utiliser la notion de puissance d'un point par rapport à un cercle.
Ok c'est plus vraiment dans le programme du lycée...
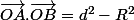
où d est la distance de O au centre du cercle cherché.
On en tire d²=2R² d'où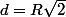
Donc le centre cherché est sur le cercle de centre O et de rayon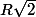
On pouvait aussi utiliser la notion de puissance d'un point par rapport à un cercle.
Ok c'est plus vraiment dans le programme du lycée...
où d est la distance de O au centre du cercle cherché.
On en tire d²=2R² d'où
Donc le centre cherché est sur le cercle de centre O et de rayon
Re: Détermine le lieu des centres des circonférences
Black Jack a écrit:Bonjour,
Equation des cercles de centre C(a;b) et de rayon R : (x-a)² + (y-b)² = R²
Cherchons les points de rencontre de ces cercles avec par exemple l'axe des ordonnées... d'équation x = 0
Il faut donc résoudre le système :
(x-a)² + (y-b)² = R²
x = 0
... donne les points de rencontre A et B cherchés : A(0 ; b + V(R²-a²)) et B(0 ; b - V(R²-a²))
avec V pour racine carrée.
vect(OA).vect(OB) = (b + V(R²-a²)) * (b - V(R²-a²))
vect(OA).vect(OB) = b² - R² + a² = a² + b² - R²
Et si on veut que vect(OA).vect(OB) = R², il faut donc que : a² + b² = 2R²
Les centres des circonférences appartiennent don à un cercle centre sur et de rayon V2 * R
... sous la contrainte qu'il faut que a <= R
Donc le lieu des centres des cercles qui coupent l'axe des ordonnées en 2 points A et B tel que vect(OA).vect(OB) sont 2 portions de cercle centré sur l'origine du repère, de rayon V2 * R et limité aux abscisses comprises dans [-a ; a]
****
On doit refaire un exercice similaire pour les cercles coupant l'axe des abscisses en 2 points ...
On devrait trouver que :
Le lieu des centres des cercles qui coupent l'axe des abscisses en 2 points A et B tel que vect(OA).vect(OB) sont 2 portions de cercle centré sur l'origine du repère, de rayon V2 * R et limité aux ordonnées comprises dans [-b ; b]
****
En regroupant les 2 lieux des centres des cercles ci dessus, le lieu des centres des cercles est le cercle complet de rayon V2.R centré sur l'origine du repère
Sur le dessin de gauche, la représentation du lieu des centres des cercles de rayon 4 répondant à l'énoncé.
Sur le dessin de droite, la construction d'un des cercles de rayon 4 avec son centre appartenant au lieu cherché sur le dessin de gauche.
Merci beaucoup pour cette explication géniale !
Juste une question. Dans ton dessin, comment as-tu trouvé les coordonnées des points A et B si R = 4 ?
Re: Détermine le lieu des centres des circonférences
Ahh j'ai compris. On prend les coordonnées du point central du cercle rouge.
Re: Détermine le lieu des centres des circonférences
yodabosten a écrit:Ahh j'ai compris. On prend les coordonnées du point central du cercle rouge.
Par exemple, ou bien on mesure OA et OB sur le dessin (et on connait la longueur d'une unité sur le dessin puisque les axes sont gradués)
On a évidemment les erreurs de lectures sur les longueurs ... mais cela permet quand même de vérifier que "à pas grand chose près", on a bien OA*OB = 16. (donc R² avec R = 4)
Ce n'est pas une preuve, mais juste une vérification suffisante pour voir que l'on ne s'est pas mis trop fort le doigt dans l'oeil dans la construction.
Bien entendu, en dessinant un autre cercle rouge ... on aurait OA et OB différents.
Mais on devrait conserver OA*OB = 16
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
