Détermination d'un ensemble avec le produit vectoriel

[Dinozzo13]

Bonjour, j'aimerai savoir si il m'est possible de faire cet exercice, sachant que j'ai quelque notions du produit vectoriel, ou alors cet exercice est d'un niveau trop élevé pour que je puisse le faire ? merci.

Soit trois points distincts de l'espace.
Déterminer l'ensemble des points du plan tels que :
.

[Nightmare]

Salut,

Ben, je sais pas, tu as essayé de le faire un peu? Avec ce que tu sais vois ce que tu peux faire. L'exercice n'est pas trop difficile non.

[Dinozzo13]

Voilà, je ne sais pas quoi faire après, peut-être introduire le point dans

[Anonyme]

Voilà, je ne sais pas quoi faire après, peut-être introduire le point dans

Plutôt dans MC non ?

[Dinozzo13]

Je ne sais pas, mais essayons :++:

Or il me semble donc :



C'est bon jusque là ?

[Anonyme]

Oui :++: je pense en tout cas (j'ai très peu travaillé avec le produit vectoriel)

Apres il me semble que tu doit introduire le barycentre de {(B,1) , (A,2)}

[Dinozzo13]

Après je pensais définir soit le barycentre des points pondérés tel que, pour tout point M de l'espace :

Donc cela équivaudrait à :

Mais après je ne vois pas comment finir :triste:

[Dinozzo13]

Oui :++: je pense en tout cas (j'ai très peu travaillé avec le produit vectoriel)

Apres il me semble que tu doit introduire le barycentre de {(B,1) , (A,2)}

:ptdr: réaction syncronisée ^^

[Anonyme]

Après je pensais définir soit le barycentre des points pondérés tel que, pour tout point M de l'espace :

Donc cela équivaudrait à :

Mais après je ne vois pas comment finir :triste:

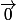
et ont même module donc ...

:ptdr: réaction syncronisée ^^

:zen:

[Nightmare]

Attention ! Le produit vectoriel n'est pas commutatif !

Edit : Mais la remarque n'a pas d'intérêt puisqu'après relecture, il n'y a pas de faute de cet ordre.

[Dinozzo13]

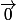
et ont même module donc ...

Ah ! Il sont colinéaires donc l'ensemble des points recherchés est une droite.

[benekire2]

C'est ça et tu peut la caractériser (parallèle a (AC) passant par G )

[Anonyme]

oui c'est bon :++:

Tant qu'on parle de produit vectoriel est ce que quelqu'un peut me dire comment on démontre la distributivité du produit vectoriel ?

[Nightmare]

Pour quelle définition ?

[Anonyme]

Pour quelle définition ?

W=U/\V

W est perpendiculaire au plan forme par U et V.
Le sens de W est déterminé par la règle de la main droite (je ne sais pas comment le décrire mathématiquement)
|W|=|U| |V| |sin (U,V)|

[Dinozzo13]

Ok, oui en effet, ce n'étais pas très dur ^^

Pourriez-vous me dire quel aurait été l'ensemble des points M de l'espace, si on a A et B deux points distincts de l'espace, tels que :

[benekire2]

selon toi ?

MA et MB colinéaires, donc M sur la droite (AB)

[Anonyme]

Ok, oui en effet, ce n'étais pas très dur ^^

Pourriez-vous me dire quel aurait été l'ensemble des points M de l'espace, si on a A et B deux points distincts de l'espace, tels que :

intercale A dans MB et tu trouve que c'est la droite (AB) si je ne m'abuse.