Déterminant de matrices
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 20:18
par nico3004 » 30 Aoû 2010, 20:18
Bonsoir, j'ai vraiment besoin d'aide...
Comment calculer le déterminant du système de cette matrice ?
ax + ay - z = 1
ax + 2y - z = 1
-x - y + az = 1
Et également comment faire pour trouver pour quelles valeurs de a le système a une, pas ou une infinité de solutions ?
Merci beaucoup d'avance !
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:25
par Dinozzo13 » 30 Aoû 2010, 20:25
Salut !
Le déterminant du système est :
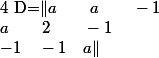
Ensuite pour le calcul, je t'invite à taper déterminant sur wikipedia
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:26
par Dinozzo13 » 30 Aoû 2010, 20:26
Ensuite, si D=0 alors le système admet soit une infinité de solutions ou aucune et si

alors il admet une solution unique.
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 20:28
par nico3004 » 30 Aoû 2010, 20:28
Merci beaucoup ;)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 20:31
par girdav » 30 Aoû 2010, 20:31
L'environnement
vmatrix est mieux (à mon sens) :

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:33
par Dinozzo13 » 30 Aoû 2010, 20:33
Ah merci, je galère a chaque fois pour tout ce qui est déterminant
:++:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:39
par Dinozzo13 » 30 Aoû 2010, 20:39
Si tu as lu la formule du déterminant alors tu vois que :

Détermine alors les racines du polynôme

:
Je t'aide, il y a une racine évidente : a=1, tu peux donc en déduire une factorisation et donc les deux autres (éventuelles) racines du polynôme.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 20:47
par girdav » 30 Aoû 2010, 20:47
Sinon, on peut faire

ce qui donne
\begin{vmatrix}a&-1\\<br />2&-1<br />\end{vmatrix}\\<br />&=(a^2-1)(-a+2)<br />\end{align}.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:48
par Dinozzo13 » 30 Aoû 2010, 20:48
Pour indication les deux autre racines sont -1 et 2 donc il y a trois valeurs de a pour lesquelles D=0 :
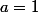
ou
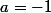
ou
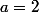
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:49
par Dinozzo13 » 30 Aoû 2010, 20:49
girdav a écrit:Sinon, on peut faire

ce qui donne
\begin{vmatrix}a&-1\\<br />2&-1<br />\end{vmatrix}\\<br />&=(a^2-1)(-a+2)<br />\end{align}.)
:ptdr: je fais avec ce que je sais :ptdr:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 20:52
par girdav » 30 Aoû 2010, 20:52
Dinozzo13 a écrit::ptdr: je fais avec ce que je sais :ptdr:
Oui, moi je triche (un peu) mais tous les coups sont permis.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:58
par Dinozzo13 » 30 Aoû 2010, 20:58
ouais, juste pour dire qu'il existe peut-être de meilleurs moyen qu'on voit en sup
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:01
par girdav » 30 Aoû 2010, 21:01
Dinozzo13 a écrit:ouais, juste pour dire qu'il existe peut-être de meilleurs moyen qu'on voit en sup
Oui, la vérité sur les déterminants sera révélée (je suppose, je n'ai pas fait sup mais j'ai vu les déterminants aussi dans les livres de sup).
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 21:36
par nico3004 » 30 Aoû 2010, 21:36
Waouw, merci beaucoup !!!! J'ai compris ^^
Et maintenant, si on veut avoir une solution, pas de solution, ou une infinité de solution pour le système comment peut-on faire ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:39
par girdav » 30 Aoû 2010, 21:39
nico3004 a écrit:Waouw, merci beaucoup !!!! J'ai compris ^^
Et maintenant, si on veut avoir une solution, pas de solution, ou une infinité de solution pour le système comment peut-on faire ?
Tu peux dans un premier temps regarder le message #3 de la discussion.
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 21:49
par nico3004 » 30 Aoû 2010, 21:49
pardon je ne l'avais pas vu, mais merci encore ^^ c'est clair je pense maintenant :we:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 21:51
par Dinozzo13 » 30 Aoû 2010, 21:51
nico3004 a écrit:ax + ay - z = 1
ax + 2y - z = 1
-x - y + az = 1
Alors lorsqu'il n'y a pas de solution

:
On calcule alors 3 autres déterminant

et
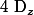
:



La solution est donc
=\(\frac{D_x}{D};\frac{D_y}{D};\frac{D_z}{D}\))
Tu remarques que pour Dx, Dy et Dz, on prends le même déterminant D auquel on remplace les colonnes des termes en x,y et z par la colonne
)
du système
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 21:55
par nico3004 » 30 Aoû 2010, 21:55
ça me semble clair mnt =) je vais faire d'autres exercices pour voir si j'ai rien compris de travers ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
