Dérivée d'une fonction irrationnelle?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
xframboise
- Messages: 4
- Enregistré le: 07 Sep 2009, 18:25
-
 par xframboise » 07 Sep 2009, 18:41
par xframboise » 07 Sep 2009, 18:41
Bonjour! Voilà j'ai un problème. Je dois résoudre une dérivée d'un quotient d'une racine cubique. Je ne sais pas si je m'exprime clairement alors pour le formuler autrement: un quotient dont le numérateur et le dénominateur sont sous la même racine. Je n'ai pas de formule pour résoudre ceci... Quelqu'un pourrait-il m'aider? Merci beaucoup!
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 07 Sep 2009, 18:45
par sky-mars » 07 Sep 2009, 18:45
Salut
si tu pouvais écrire la fonction, on pourrait peut être t'aider ....
Pour info racine rubique c'est la puissance

et tu dérives
' = n u' u ^{n-1})
avec
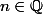
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Sep 2009, 18:47
par girdav » 07 Sep 2009, 18:47
Bonjour.
Si je comprends bien on veut dériver une fonction de la forme
}{v(x)}\)^{\fr 13})
? C'est une composée.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 07 Sep 2009, 18:48
par sky-mars » 07 Sep 2009, 18:48
Pour la composée tu utilises la formule du cours:
(uov)'(x) = v ' (x) u ' ( v(x) )
-
xframboise
- Messages: 4
- Enregistré le: 07 Sep 2009, 18:25
-
 par xframboise » 07 Sep 2009, 18:49
par xframboise » 07 Sep 2009, 18:49
La fonction c'est: radical de (x+1)/(2x-1)
-
xframboise
- Messages: 4
- Enregistré le: 07 Sep 2009, 18:25
-
 par xframboise » 07 Sep 2009, 18:51
par xframboise » 07 Sep 2009, 18:51
Oui excusez moi je me suis trompée dans ma première question... La dérivée que je dois calculer est celle de la fonction que je viens de mettre...
Et c'est le radical de tout le quotient
-
xframboise
- Messages: 4
- Enregistré le: 07 Sep 2009, 18:25
-
 par xframboise » 07 Sep 2009, 19:50
par xframboise » 07 Sep 2009, 19:50
Personne? :triste:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 07 Sep 2009, 20:48
par Ericovitchi » 07 Sep 2009, 20:48
Si je comprends bien tu veux calculer la dérivée de

?
Il me semble que l'on t'a donné toutes les indications nécessaires dans les précédents posts ? Essayes !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
