Dérivée et primitives

[Anonyme]

Je reposte mon énoncé après modification

Bonjour,

mon énoncé est :

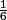
soit f(x) = x(x + )*

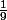
1) Justifier que f est deux fois dérivable sur R et exprimer f'(x) et f"(x)
2) Montrer que pr tt x de R : f"(x) -f(x) -2f(x) = -x*

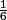
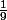
1) Je ne suis pas sur de mes résultats, j'ai simplifier l'expression de f(x) en f(x) = (x² + x)*


f'(x) = + +

f"(x) = +
=
=

2) Pour la question 2 j'arrive à

En continuant j'arrive a *(-18x^2 - 17x - 15) = 0

Je ne sais pas du tout si mon calcul est juste alors j'hésite à le continuer :triste:

Pouvez vous m'aider svp

[Equiangle]

Bonjour,

Je pense que tu t'es trompé dans le calcul des dérivées.

Pour f'(x), on a f(x)= (1/6*x² + 1/9*x)*e^(-x)

C'est de la forme f(x)=U*V donc sa dérivée sera de la forme f'(x)=U'V + UV' avec U=1/6*x² + 1/9*x et V=e^(-x) donc U'= 1/3*x + 1/9 et V' = -e^(-x)

Je trouve f'(x)= e^(-x)*(-x²/6 + 2x/9 + 1/9)
vérifie tes calculs, à mon avis tu as fait une erreur de signe.

[Huppasacee]

quelle est la dérivée de ?

[Anonyme]

quelle est la dérivée de ?

La dérivée de l'exponentielle est elle même

[aeon]

sauf que ce n'est pas e^x mais e^-x !

[Anonyme]

sauf que ce n'est pas e^x mais e^-x !

Ca ne change rien ?! e(-x)' = e(-x) non ?

[aeon]

eh bien justement non.

(fog(x))' = g'(x) * f'og(x)

avec f(x) = e^x et g(x) = -x

on obtient : (e(-x))' = (-x)' * e'(-x) = -1 * e(-x) = - e^(-x)

[Huppasacee]

En effet
ici on a exp ( u )

dont la dérivée est

u ' * exp (u)

ceci est vrai aussi pour sin u ( et non pas sin x )

la dérivée est
u ' cos u

etc .

[Anonyme]

Ah d'accord je pensais pas du tout à ça, merci

J'ai bien fait de ne pas continuer :cry: