Dérivé et variation fonction rationnelle.

par **novicemaths** » 06 Avr 2015, 11:33

Bonjour

Voici ci-dessous une fonction, je sois établir un tableau de variation.

On la dérive.

Ma question est doit-on calculer ainsi :

=

Cordialement

par **Ericovitchi** » 06 Avr 2015, 12:18

heu non, la dérivée de 1/x² c'est -2/x^3 (dérive comme x^(-2) )

(et puis 1/A + 1/B ça n'a jamais fait 1/(A+B) !!)

par **zygomatique** » 06 Avr 2015, 12:20

novicemaths a écrit:Bonjour

Voici ci-dessous une fonction, je sois établir un tableau de variation.

On la dérive.

Ma question est doit-on calculer ainsi : =

Cordialement

salut

la réponse à ta question est : qu'as-tu appris au collège ? :marteau:

par **novicemaths** » 06 Avr 2015, 15:23

Bonjour

Donc, ca fait

Question, pour établir la variation de f, doit-on les additionner?

A+

par **zygomatique** » 06 Avr 2015, 16:33

il faut factoriser (pour étudier le signe) donc réduire au même dénominateur ...

par **novicemaths** » 09 Avr 2015, 15:27

Bonjour

Oui, mais si on fait ça ca donne:

Soit

Après je ne pas comment faire

=?

Cordialement

par **Shew** » 09 Avr 2015, 15:33

novicemaths a écrit:Bonjour

Oui, mais si on fait ça ca donne:

Soit

Après je ne pas comment faire =?

Cordialement

Il y'a plus simple on se concentre uniquement sur

et on le traite soit :

par **novicemaths** » 10 Avr 2015, 07:29

Bonjour

Est-ce que

Là, je cherche des cours sur le net sur la manipulation de de fraction pour les fonctions

A+

par **zygomatique** » 10 Avr 2015, 08:52

il est temps de retourner en collège et réviser le calcule algébrique ....

par **Pseuda** » 10 Avr 2015, 14:09

Hum :

cela fait

De même :

+

cela ne fait pas :

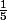
. Il faut mettre au même dénominateur.

Il s'agit de notions de l'école primaire. Mon conseil : revoir tout le programme de mathématiques depuis les classes primaires, et surtout comprendre les formules, si tu veux les retenir.

par **novicemaths** » 11 Avr 2015, 04:47

Bonjour

Je sais que

Dans les fractions algébriques c'est les x qui me perturbe.

A +

par **Pseuda** » 11 Avr 2015, 17:04

Avec les x, c'est EXACTEMENT la même chose. Si tu as un doute sur un calcul avec des lettres, tu peux prendre des nombres et voir si ça colle, ou revenir provisoirement aux nombres (par exemple calculer

=

) puis revenir vers les lettres.

Pour t'aider, il y a les cours du CNED avec des exercices et des corrigés (parfois) : choisis tout ce qui concerne le calcul numérique et le calcul littéral depuis la 6ème :

http://www.academie-en-ligne.fr/default.aspx

par **novicemaths** » 16 Avr 2015, 03:38

Bonjour

Est-ce que dans ce type de fonction on doit applique f'(x)=u'(x)v(x)+u(x)v'(x) ?

A +

Dérivé et variation fonction rationnelle.

Dérivé et variation fonction rationnelle.

Qui est en ligne