Bonjour
Quand j'ai
f '(x)=9x²-14x+2
POur trouver la dérivé, je dois garder en tête que la dérivée de:
fonction carré : c'est le double
Que l'orsqu'il y a x c'est * 1
Et que lorsqu'il y ni a qu'une constante c'est 0,
Or je pense m'être embrouiller car si je suivais ma logique ( qui n'en n'est pas une )
cela donnerai
9 * 2x -14*1 ( et on retire le 0) = 18x -14
18*1-14= 4
Cependant dans ma correction, il y a écrit : 9*1carré-14*1 +2 = -3
Et la je suis perdu ! J'ai besoin d'un coup de main !
Dérivé et tangente
13 messages
- Page 1 sur 1
Bien en faite , je devais déterminer l'équation de la tangente
avec pour équation 3xcube-7xcarré+2x+4
donc f'(1) ( x-1) + f(1)
avec f(1) = 2
donc f'(x) = 9xcarré -14x +2
donc f'(1) = 9*1carré-14*1+2 = -3
Pourquoi cela ?
POurquoi n'ai je pas continuer à trouver la dérivé complète de f ?
Pourriez-vuios me donnez un exercie similiaire à faire pour m'entraîner ?
avec pour équation 3xcube-7xcarré+2x+4
donc f'(1) ( x-1) + f(1)
avec f(1) = 2
donc f'(x) = 9xcarré -14x +2
donc f'(1) = 9*1carré-14*1+2 = -3
Pourquoi cela ?
POurquoi n'ai je pas continuer à trouver la dérivé complète de f ?
Pourriez-vuios me donnez un exercie similiaire à faire pour m'entraîner ?
> xezil
"POurquoi n'ai je pas continuer à trouver la dérivé complète de f ?"
>>> qu'appelles tu dérivée complète ?
Soit f une fonction dérivable. La tangente au point d'abscisse 'a' à la courbe repr de f a pour équation :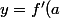(x-a) + f(a)) .
.
Ici tu as = 3x^3 + 7x^2 + 2x + 4)
Sa dérivée est bien = 9x^2 + 14x + 2)
Effectivement, si tu redérives tu as = 18x + 14) mais ça ne sert à rien pour le calcul de l'équation de la tgte (on appelle f'' la "dérivée seconde").
mais ça ne sert à rien pour le calcul de l'équation de la tgte (on appelle f'' la "dérivée seconde").
Donc, en 1 par exemple, la tgte a pour équa y = f'(1)(x-1)+f(1)
"POurquoi n'ai je pas continuer à trouver la dérivé complète de f ?"
>>> qu'appelles tu dérivée complète ?
Soit f une fonction dérivable. La tangente au point d'abscisse 'a' à la courbe repr de f a pour équation :
Ici tu as
Sa dérivée est bien
Effectivement, si tu redérives tu as
Donc, en 1 par exemple, la tgte a pour équa y = f'(1)(x-1)+f(1)
Je connais mes formules mais je ne saivais pas jusqu'ou je devais dérivé !
Aparamment je n'ai qu'a dérivé qu'une fois et cela s'apelle la dérivée seconde ?
POur trouver la tangente je ne dois pas allez plus loin que la dérivée seconde est-ce bien cela ?
Pourriez vous me redonnez un exercice similiaire à faire ?
Aparamment je n'ai qu'a dérivé qu'une fois et cela s'apelle la dérivée seconde ?
POur trouver la tangente je ne dois pas allez plus loin que la dérivée seconde est-ce bien cela ?
Pourriez vous me redonnez un exercice similiaire à faire ?
xezil0789 a écrit:Je connais mes formules mais je ne saivais pas jusqu'ou je devais dérivé !
Aparamment je n'ai qu'a dérivé qu'une fois et cela s'apelle la dérivée seconde ?
POur trouver la tangente je ne dois pas allez plus loin que la dérivée seconde est-ce bien cela ?
Pourriez vous me redonnez un exercice similiaire à faire ?
La tangente en un point est donnée par le nombre dérivé de la fonction en ce point.
Une tangente est d'abord une droite et une droite a pour équation y=mx+p. Ben m (coefficient directeur) est justement le nombre dérivé.
Exemple:
Tangente en 0: m=0
Tangente en 1: m=3
Tangente en 2: m=12
Tangente en 3: m=27
Si on doit donner une formule générale de la fonction qui à m donne f'(m), alors pour
Si à partir de f'(x)=3x² tu t'amuses à redériver (t'as le droit), ça te donnera f''(x)=6x. Mais cette dérivée seconde (t'as dérivé 2 fois f) ne sert à rien dans le calcul de la tangente pour Cf (Cf=Courbe représentative de f).
Tu veux un exercice ?
PS: Si tu ne sais pas dériver
xezil0789 a écrit:y = f ' ( a) (x-a) + f (a)
avec f(a) = 1
f ' (x) = -1/xcarré
f' (1) = -1
y = -1 ( x-1 ) + 1
y = -x+1+1
y= -x+2
Aurais-je trouver le bon résultat pour l'exemple n°1 ?
Voilà. T'as compris le calcul. Tout ce qui te reste ensuite est d'apprendre les dérivées.
Cependant, si tu réfléchis bien, une grande partie des formules de calcul peuvent se réduire seulement à celle-là:
En effet, racines et fractions peuvent toujours s'écrire sous une forme de puissance. Ensuite bien sûr il faut savoir dériver une somme ou un produit de fonctions mais déjà, la formule principale répond à beaucoup de problèmes
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
