Derivé
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 02 Déc 2006, 15:29
par juju78 » 02 Déc 2006, 15:29
bonjour on a f
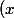= (x^3+1)^4 . Vx)
(V= racine)
On me demande la derivée, je fais donc:
=4(x^3+1)^33x^2.Vx + 1/(2Vx).(x^3+1)^4)
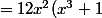^3.Vx + (x^3+1)^4/(2Vx))
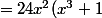^3x + (x^3+1)^4 / (2Vx))
C'est ca?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 02 Déc 2006, 15:50
par anima » 02 Déc 2006, 15:50
juju78 a écrit:bonjour on a f
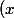= (x^3+1)^4 . Vx)
(V= racine)
On me demande la derivée, je fais donc:
=4(x^3+1)^33x^2.Vx + 1/(2Vx).(x^3+1)^4)
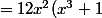^3.Vx + (x^3+1)^4/(2Vx))
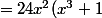^3x + (x^3+1)^4 / (2Vx))
C'est ca?
A mon avis, tu t'es emballé (ou je me suis emballé). Je trouve:
^3[12x^2\sqrt{x} + \frac{x^3+1}{2\sqrt{x}}])
-
stef
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Avr 2006, 14:26
-
 par stef » 02 Déc 2006, 16:45
par stef » 02 Déc 2006, 16:45
Moi je trouve
^3 + (x^3+1)^4/2Vx)
où V est racine carré.
-
Joebon
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Déc 2006, 20:12
-
 par Joebon » 02 Déc 2006, 17:08
par Joebon » 02 Déc 2006, 17:08
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 02 Déc 2006, 17:59
par anima » 02 Déc 2006, 17:59
le ^4 du deuxieme (x^3+1) a disparu. Sinon, je me suis permis de mettre (x^3+1)^3 en facteur, cela permet si il y a besoin d'avoir de facon "simple" les racines :zen:
-
Joebon
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Déc 2006, 20:12
-
 par Joebon » 02 Déc 2006, 18:02
par Joebon » 02 Déc 2006, 18:02
En effet, j'ai oublié la racine carré à la troisième ligne.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités