DM DERIVATION 1es (bloqué sur la fin)
13 messages
- Page 1 sur 1
DM DERIVATION 1es (bloqué sur la fin)
Bonjour, je suis en 1ère ES et j'ai un dm à faire pour s'entraîner pour la prochaine interro mardi prochain. J'ai du mal en maths mais ça allait à peu près jusqu'à cette leçon sur les dérivations. Je dois absolument comprendre pour la prochaine interro de rattrapage car j'ai eu 4 à la dernière! Pouvez-vous me dire si ce que j'ai fait est bon et m'expliquer pour les questions que je ne comprends pas SVP.
EXERCICE 1
Soient deux fonctions définies sur R par f(x)=x²+2x+3 et g(x)=-1/2x²+1. On donne la représentation graphique de ces deux fonctions ci-dessous :
http://imagesia.com/derivation-003_s66q
Question intermédiaire indépendante de l'exercice:
Soient deux droites (d1) : y=m1x+p1 et (d2) : y=m2x+p2
Quelles sont les conditions sur m1, m2, p1 et p2 pour que les deux droites soient confondues ?
Ma réponse : Je pense que les coefficients directeurs m1 et m2 doivent être égaux et p1=p2 (mais pas du tout convaincu!!)
Partie A :
1) Etudier les variations de la fonction f
Ma réponse :
f(x)=x²+2x+3
f '(x)=1*2*x^2-1+2*1*x^1-1+0=2x+2
f '(x)=0
2x+2=0
2x=-2
x=-2/2
x=-1
Tableau de variation :
http://imagesia.com/derivation-001_s66r
2) Etudier les variations de la fonction g
Ma réponse :
g(x)=-1/2x²+1
g '(x)=-1/2*2*x^2-1+0=-x
g '(x)=0
-x=0
Mes calculs sont bons ?
Tableau de variation :
http://imagesia.com/derivation-002_s66s
3) En déduire quelle est la courbe représentative de la fonction f et donc quelle est celle de g.
Ma réponse : La courbe représentative de la fonction f est donc la première en haut. Celle de la fonction g est la courbe du bas.
Partie B :
Le but de cet partie est de déterminer s'il existe des tangentes communes à ces deux courbes, et le cas échéant, de déterminer l'équation de la (des) tangente(s).
Soient A(a,f(a)), un point appartenant à la courbe représentative de f, et B (b, g(b)), un point appartenant à la courbe représentative de g.
1) Démontrer que l'expression générale de l'équation de la tangente à la courbe représentative de f, au point d'abscisse A est :
y=(2a+2)x-a²+3
Ma réponse :??
2) Démontrer que l'expression générale de l'équation de la tangente à la courbe représentative de g, au point d'abscisse B est :
y=-bx+(1/2)b²+1
Ma réponse : -bx correspond à g'(x) et (1/2)b²+1 correspond à g(x). Je ne sais pas comment l'expliquer autrement???
3) Déterminer, à l'aide de la résolution d'un système de deux équations, les équations des deux tangentes communes aux deux courbes.
Là je ne sais pas comment m'y prendre? Quelles formules je dois prendre ?
Merci d'avance à ceux qui voudront bien m'aider jusqu'au bout pour ce DM.
EXERCICE 1
Soient deux fonctions définies sur R par f(x)=x²+2x+3 et g(x)=-1/2x²+1. On donne la représentation graphique de ces deux fonctions ci-dessous :
http://imagesia.com/derivation-003_s66q
Question intermédiaire indépendante de l'exercice:
Soient deux droites (d1) : y=m1x+p1 et (d2) : y=m2x+p2
Quelles sont les conditions sur m1, m2, p1 et p2 pour que les deux droites soient confondues ?
Ma réponse : Je pense que les coefficients directeurs m1 et m2 doivent être égaux et p1=p2 (mais pas du tout convaincu!!)
Partie A :
1) Etudier les variations de la fonction f
Ma réponse :
f(x)=x²+2x+3
f '(x)=1*2*x^2-1+2*1*x^1-1+0=2x+2
f '(x)=0
2x+2=0
2x=-2
x=-2/2
x=-1
Tableau de variation :
http://imagesia.com/derivation-001_s66r
2) Etudier les variations de la fonction g
Ma réponse :
g(x)=-1/2x²+1
g '(x)=-1/2*2*x^2-1+0=-x
g '(x)=0
-x=0
Mes calculs sont bons ?
Tableau de variation :
http://imagesia.com/derivation-002_s66s
3) En déduire quelle est la courbe représentative de la fonction f et donc quelle est celle de g.
Ma réponse : La courbe représentative de la fonction f est donc la première en haut. Celle de la fonction g est la courbe du bas.
Partie B :
Le but de cet partie est de déterminer s'il existe des tangentes communes à ces deux courbes, et le cas échéant, de déterminer l'équation de la (des) tangente(s).
Soient A(a,f(a)), un point appartenant à la courbe représentative de f, et B (b, g(b)), un point appartenant à la courbe représentative de g.
1) Démontrer que l'expression générale de l'équation de la tangente à la courbe représentative de f, au point d'abscisse A est :
y=(2a+2)x-a²+3
Ma réponse :??
2) Démontrer que l'expression générale de l'équation de la tangente à la courbe représentative de g, au point d'abscisse B est :
y=-bx+(1/2)b²+1
Ma réponse : -bx correspond à g'(x) et (1/2)b²+1 correspond à g(x). Je ne sais pas comment l'expliquer autrement???
3) Déterminer, à l'aide de la résolution d'un système de deux équations, les équations des deux tangentes communes aux deux courbes.
Là je ne sais pas comment m'y prendre? Quelles formules je dois prendre ?
Merci d'avance à ceux qui voudront bien m'aider jusqu'au bout pour ce DM.
Bonjour,
Tout le début est bon =).
L'équation de la tangente à la courbe au point d'abscisse a se calcule à l'aide de la formule :
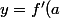 (x - a) + f(a))
Pour la question 2 : même chose :
 (x - b) + g'(b))
Pour la question 3 il faudra donc résoudre le système composé des deux équations que tu auras déterminer dans 1) et 2).
Tout le début est bon =).
1) Démontrer que l'expression générale de l'équation de la tangente à la courbe représentative de f, au point d'abscisse A est :
y=(2a+2)x-a²+3
L'équation de la tangente à la courbe au point d'abscisse a se calcule à l'aide de la formule :
Pour la question 2 : même chose :
Pour la question 3 il faudra donc résoudre le système composé des deux équations que tu auras déterminer dans 1) et 2).
Bonjour et merci de m'avoir répondu. Oui mais jusqu'à présent les seuls exercices que j'ai fait avec le calcul de l'équation d'une tangente on nous donner la valeur de a du coup là ça me bloque (il ne faut pas grand chose pour me bloquer). Je dois prendre une valeur au hasard par ex -1? Même ma question intermédiaire est bonne ?
stephane61 a écrit:Bonjour et merci de m'avoir répondu. Oui mais jusqu'à présent les seuls exercices que j'ai fait avec le calcul de l'équation d'une tangente on nous donner la valeur de a du coup là ça me bloque (il ne faut pas grand chose pour me bloquer). Je dois prendre une valeur au hasard par ex -1? Même ma question intermédiaire est bonne ?
Question intermédiaire : pour que deux droites soient confondues, il faut qu'elles aient le même coefficient directeur et la même ordonnée à l'origine.
En fait il ne faut pas remplacer 'a' mais l'utiliser.
Voilà pour le premier.
Pour la seconde question il te suffit d'appliquer la même méthode mais avec g(x).
Oui c'est ok pour 1) et 2)
Pour la 3) je vais te poser une question à laquelle tu as déjà répondu en fait :) :
Soient deux droites (d1) :
y=(2a + 2)x - a² + 3
et (d2) :
y = -bx + 1/2 b² + 1
Quelles sont les conditions sur (2a + 2), -b et (-a² + 3), (1/2 b² + 1) pour que les deux droites soient confondues ?
Pour la 3) je vais te poser une question à laquelle tu as déjà répondu en fait :) :
Soient deux droites (d1) :
y=(2a + 2)x - a² + 3
et (d2) :
y = -bx + 1/2 b² + 1
Quelles sont les conditions sur (2a + 2), -b et (-a² + 3), (1/2 b² + 1) pour que les deux droites soient confondues ?
Pourquoi 2a+2=-b et -a²+3=1/2b²+1 ? Désolé je suis long à comprendre. Pourquoi c'est pas (2a+2)x-a²+3 et -bx+1/2b²+1 qu'il faut résoudre? De toute façon que ce soit l'un ou l'autre je ne sais pas comment faire... Merci pour votre patience. C'est pas faute d'essayer.
2a+2=-b c'est f '(x)=g '(x) ? donc 2x+2=-x?
2a+2=-b c'est f '(x)=g '(x) ? donc 2x+2=-x?
Si on reprend :
Cela fonctionne si m1 = m2 et p1 = p2.
Sachant qu'on a 2 équations :
y=(2a + 2)x - a² + 3
y = -bx + 1/2 b² + 1
Donc si on se ramène à la citation ci-dessus :
m1 = (2a + 2)
p1 = (-a² + 3)
m2 = -b
p2 = 1/2 b² + 1
Donc pour trouver a et b il suffit de résoudre le système :
m1 = m2
p1 = p2
C'est à dire :
(2a + 2) = -b
(-a² + 3) = 1/2 b² + 1
Tu sais normalement résoudre un système.
Astuce : essaye d'exprimer b en fonction de a puis de remplacer dans la seconde équation.
Soient deux droites (d1) : y=m1x+p1 et (d2) : y=m2x+p2
Quelles sont les conditions sur m1, m2, p1 et p2 pour que les deux droites soient confondues ?
Cela fonctionne si m1 = m2 et p1 = p2.
Sachant qu'on a 2 équations :
y=(2a + 2)x - a² + 3
y = -bx + 1/2 b² + 1
Donc si on se ramène à la citation ci-dessus :
m1 = (2a + 2)
p1 = (-a² + 3)
m2 = -b
p2 = 1/2 b² + 1
Donc pour trouver a et b il suffit de résoudre le système :
m1 = m2
p1 = p2
C'est à dire :
(2a + 2) = -b
(-a² + 3) = 1/2 b² + 1
Tu sais normalement résoudre un système.
Astuce : essaye d'exprimer b en fonction de a puis de remplacer dans la seconde équation.
Bonsoir merci d'être revenu voir. J'ai compris cette fois comment vous êtes arrivé au système à résoudre!! Mais j'ai honte car je ne sais pas comment résoudre ce système. Je n'en ai pas encore fait cette année. En seconde je l'avais fait mais pour trouver le point d'intersection de deux droites et là ça fait pas pareil. Je ne vois pas comment exprimer b en fonction de a ? Après je pense qu'avec le résultat trouvé on remplace les x dans la seconde équation. Si vous avez encore la patience...
J'aurai jamais réussi à trouver ça !! On l'a pas fait en cours en plus. Oui je vais essayer de le refaire et vérifier les calculs demain en mettant au propre tout ça et à tête reposée. Je vais continuer à faire mes petites fiches!! Grand merci à vous car ça m'a aidé à comprendre plusieurs choses qui n'étaient pas claires pour moi notamment avec y=mx+p. J'espère que le prof ne rajoutera pas des petites surprises comme la dernière question à l'interro!!! Merci pour votre aide et bonne nuit!
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
