Bonjour je bloque sur cette exo je comprends pas comment faire
f est la fonction définie et dérivable sur R par f(x) = (1+x+x²+x(au cube) )e(puissance -2x+1)
démontrer que pour tout réel x>1, 1<x<x²<x(au cuve)
Démontrer que pour tout réel x>1
3 messages
- Page 1 sur 1
Re: démontrer que pour tout réel x>1
bonsoir
comme x>1, x est strictement positif. On peut donc multiplier chaque membre de l'inégalité par x.
il vient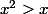
comme x>1, x est strictement positif. On peut donc multiplier chaque membre de l'inégalité par x.
il vient
Re: démontrer que pour tout réel x>1
Merci beaucoup pour votre réponse aussi rapide, je bloque pas mal sur mon dm qui est a rendre pour demain...
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
