Voici la figure :
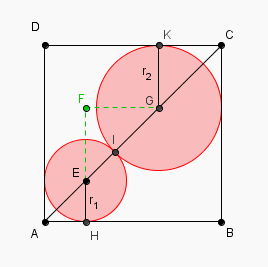
ABCD est un carré de côté 1
on construit les cercles C1 et C2 entièrement inclus dans le carré tels que :
-les points E et G centres respectifs de C1 et C2 sont sur la diagonale [AC];
-les cercles sont tangents extérieurement en I ;
-les droites (AB) et (AD) sont tangentes au cercle C1 ;
-les droites (CB) et (CD) sont tangentes au cercle C2 .
On appelle S la somme des aires des disques délimités par les cercle C1 et C2.
L'objectif du tp est de conjecturer les positions des points E et G sur le segment [AC] pour lesquelles les valeurs maximale et minimale de l aire S sont atteintes puis de demontrer cette conjecture .
On appelle r1 et r2 les rayons des cercles c1 et c2
Voici la premiere question démontrer que r1(racine de 2)+r1+r2+r2(racine de2)=racine de 2) . Que peut on déduire pour r1+r2.
La deuxième : Par des considérations géométrique démontrer que les valeurs maxi et mini que peut prendre le rayon d'un des cercles sont 1/2 et 3-2(racine de 2)/2.
La troisième : on pose x = r1 et on considère la fonction f donnant l'aire S en fonction de x. Déterminer le domaine de définition de f puis conjecturer les positions de E et les valeurs de r1 associées pour lesquelles les valeurs Max et mini de l'aire S sont atteintes .
J'ai vraiment besoin d'aide . Ça serait sympa de m'aider .
