je dois faire la preuve/démonstration de sin(a+b)=cos(b)sin(a)+sin(b)cos(a) et je n'ai aucune idée de comment faire
merci d'avance
Démonstration sin(a+b)=cos(b)sin(a)+sin(b)cos(a)
5 messages
- Page 1 sur 1
Démonstration sin(a+b)=cos(b)sin(a)+sin(b)cos(a)
par nessie » 21 Jan 2017, 15:02
Bonjour
je dois faire la preuve/démonstration de sin(a+b)=cos(b)sin(a)+sin(b)cos(a) et je n'ai aucune idée de comment faire
merci d'avance
je dois faire la preuve/démonstration de sin(a+b)=cos(b)sin(a)+sin(b)cos(a) et je n'ai aucune idée de comment faire
merci d'avance
Re: Démonstration sin(a+b)=cos(b)sin(a)+sin(b)cos(a)
par mathelot » 21 Jan 2017, 15:57
Soient deux points sur le cercle trigonométrique )
et .)
où a et b sont deux réels
On fait le produit scalaire de
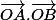
de deux manières
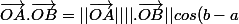= cos(a)cos(b)+sin(a)sin(b))
d'où
= cos(a)cos(b)+sin(a)sin(b))
ensuite=cos(\frac{\pi}{2}-x))
et =sin(\frac{\pi}{2}-x))
=cos(\frac{\pi}{2}-a-b)=cos((\frac{\pi}{2}-a)-b))
-b)=cos(\frac{\pi}{2}-a)cos(b)+sin(\frac{\pi}{2}-a)sin(b))
=sin(a)cos(b)+cos(a)sin(b))
où a et b sont deux réels
On fait le produit scalaire de
d'où
ensuite
Modifié en dernier par mathelot le 21 Jan 2017, 16:43, modifié 3 fois.
Re: Démonstration sin(a+b)=cos(b)sin(a)+sin(b)cos(a)
par mathelot » 21 Jan 2017, 16:13
2eme méthode avec l'exponentielle complexe:
a et b sont deux réels:
}=e^{ia}.e^{ib})
en prenant les parties imaginaires des deux membres:
=\Im((cosa+isina)(cos(b)+isin(b))))
=cosa sinb+sin(a)cos(b))
a et b sont deux réels:
en prenant les parties imaginaires des deux membres:
Re: Démonstration sin(a+b)=cos(b)sin(a)+sin(b)cos(a)
par mathelot » 21 Jan 2017, 16:27
pour la démo 1, tu as besoin d'un produit scalaire sur 
Re: Démonstration sin(a+b)=cos(b)sin(a)+sin(b)cos(a)
par Ben314 » 21 Jan 2017, 18:22
Salut,
Perso, j'aurais principalement raisonné sur le cercle trigo. :
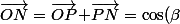\vec{u}\!\!+\!\sin(\beta)\vec{v}=\cos(\beta)\Big(\cos(\alpha)\vec{i}\!\!+\sin(\alpha)\vec{j}\Big)+\sin(\beta)\Big(\cos(\alpha\!+\!\frac{\pi}{2}))\vec{i}\!\!+\sin(\alpha\!+\!\frac{\pi}{2})\vec{j}\Big))
Perso, j'aurais principalement raisonné sur le cercle trigo. :
- Capture-1.png (16.35 Kio) Vu 2630 fois
Modifié en dernier par Ben314 le 21 Jan 2017, 18:44, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 106 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :