Demonstration degalites
15 messages
- Page 1 sur 1
demonstration degalites
Démontrer les egalites suivantes :
1) rc de 5 - rc de 3 = rc(8-2rc de 15)
2) rc(de 4 + 2 rc 3) + rc(4-2 rc 3) = 2rc3
Help please !
1) rc de 5 - rc de 3 = rc(8-2rc de 15)
2) rc(de 4 + 2 rc 3) + rc(4-2 rc 3) = 2rc3
Help please !
Ericovitchi a écrit:oui mais développe les deux cotés si tu veux montrer qu'ils sont égaux. là tu ne démontres rien du tout.
et puis c'est pas ça c'est montrer que (V5-V3)²=V(8-2V15)²
et (V(4+2V3) + V(4-2V3))² = (2V3)²
Ah oui d'accord mais est ce Que cest possible que l'égalité soit fausse ? Je veux dire qu'on ne trouve pas le même résultats en mettant au carre ?
je vois que l'on t'a déjà répondu sur des égalités presque identiques : http://www.maths-forum.com/demonstration-d-egalites-166493.php
donc tu ne devrais plus hésiter.
Si on ne trouve pas le même résultat, c'est que l'égalité est fausse.
(mais comme on t'a demandé de la démontrer, c'est peu probable)
donc tu ne devrais plus hésiter.
Si on ne trouve pas le même résultat, c'est que l'égalité est fausse.
(mais comme on t'a demandé de la démontrer, c'est peu probable)
salut
il est temps de t'y mettre ...
http://www.maths-forum.com/demonstration-d-egalites-166493.php
...
il est temps de t'y mettre ...
http://www.maths-forum.com/demonstration-d-egalites-166493.php
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
[quote="Ericovitchi"]je vois que l'on t'a déjà répondu sur des égalités presque identiques : http://www.maths-forum.com/demonstration-d-egalites-166493.php
donc tu ne devrais plus hésiter.
Si on ne trouve pas le même résultat, c'est que l'égalité est fausse.
(mais comme on t'a demandé de la démontrer, c'est peu probable)[/QUOT
Oui j'ai du mal !
Oui c'est vrai...
donc tu ne devrais plus hésiter.
Si on ne trouve pas le même résultat, c'est que l'égalité est fausse.
(mais comme on t'a demandé de la démontrer, c'est peu probable)[/QUOT
Oui j'ai du mal !
Oui c'est vrai...
zygomatique a écrit:salut
il est temps de t'y mettre ...
http://www.maths-forum.com/demonstration-d-egalites-166493.php
...
En effet ... En quelle classe fait-on cela si vous savez ?
en classe de troisième ... lorsqu'on a appris à faire du calcul mental (apprendre = pratiquer :lol3: )
donc lorsqu'on connaît les identités remarquables (et les racines carrées, à savoir que tout nombre positif est le carré de sa racine carrée ) ça pète à la gueule que ::
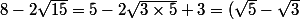^2 = (\sqrt 3 - \sqrt 5)^2)
:ptdr:
bon ... faut aussi savoir ses tables de multiplication :: 15 = 3 * 5 et que deux nombres opposés ont même carré ...
que des trivialités de collège en somme ...
:ptdr:
donc lorsqu'on connaît les identités remarquables (et les racines carrées, à savoir que tout nombre positif est le carré de sa racine carrée ) ça pète à la gueule que ::
:ptdr:
bon ... faut aussi savoir ses tables de multiplication :: 15 = 3 * 5 et que deux nombres opposés ont même carré ...
que des trivialités de collège en somme ...
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:en classe de troisième ... lorsqu'on a appris à faire du calcul mental (apprendre = pratiquer :lol3: )
donc lorsqu'on connaît les identités remarquables (et les racines carrées, à savoir que tout nombre positif est le carré de sa racine carrée ) ça pète à la gueule que ::
:ptdr:
bon ... faut aussi savoir ses tables de multiplication :: 15 = 3 * 5 et que deux nombres opposés ont même carré ...
que des trivialités de collège en somme ...
:ptdr:
Ahh pardon monsieur je sais tout ! Merci pour laide
work03 a écrit:Ahh pardon monsieur je sais tout ! Merci pour laide
ce n'est pas monsieur je sais tout c'est monsieur je sais tout ... du collège !!! :ptdr: ... et je n'ai pas oublié ...
... enfin presque tout ... nul n'étant parfait ... mais j'ai eu des bons profs qui m'ont bien instruit en la mathématique ...
:lol3:
et pour répondre à ta question il suffit enfin de savoir que
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:ce n'est pas monsieur je sais tout c'est monsieur je sais tout ... du collège !!! :ptdr: ... et je n'ai pas oublié ...
... enfin presque tout ... nul n'étant parfait ... mais j'ai eu des bons profs qui m'ont bien instruit en la mathématique ...
:lol3:
et pour répondre à ta question il suffit enfin de savoir que... :++:
:lol3:
Oui en effet ce qui est peut être pas mon cas en tout cas merci :id: :++:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
