Bonjour à tous,
j'ai un devoir à remettre pour la semaine prochaine mais je n'arrive pas à le faire.
Aidez-moi SVP si vous avez un peu de temps.
voici l'énonce:
-Dessine la courbe qui en coord. polaires a pour équation et observer les symétries éventuelles.
r²= sin2;) (sin2;) = 2sin;).cos;))
-Interprêter dx/d;) et dy/d;) et Calculer l'équation en coord. cartésienne
voila ce que j'ai trouvé pour l'équation
r²= sin2;)
r²= 2sin;).cos;)
x²+y²= 2xy / x²+y² ------> r²= x²+y³
(x²+y²)²= 2xy
x4+y4+2x²y²-2xy=0
x4+y4+2xy(xy-1)=0
je ne sais pas si c'est correct. Il me reste à tracer la courbe.
Vous pouvez me donner des pistes pour la symétrie et pour x/d;) et dy/d;).
MERCI d'avance :help:
Coordonnées Polaires
9 messages
- Page 1 sur 1
Bonjour,
Pour les symétries et le tracé de la courbe, une première symétrie saute aux yeux, en effet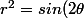) implique pour une valeur donnée de
implique pour une valeur donnée de  que
que  prend la valeur
prend la valeur }) et la valeur
et la valeur }) ce qui donne quoi comme symétrie ?
ce qui donne quoi comme symétrie ?
Ensuite, il faut retenir que le sinus est périodique on peut donc restreindre l'intervalle décrit par
périodique on peut donc restreindre l'intervalle décrit par  à un intervalle de longueur
à un intervalle de longueur  , prenons par exemple
, prenons par exemple  et je te laisse poursuivre.
et je te laisse poursuivre.
Et pour et
et  que valent
que valent  et
et  en fonction de
en fonction de  et
et  ? Donc la dérivée ?
? Donc la dérivée ?
Pour les symétries et le tracé de la courbe, une première symétrie saute aux yeux, en effet
Ensuite, il faut retenir que le sinus est
Et pour
Arnaud-29-31 a écrit:Bonjour,
Pour les symétries et le tracé de la courbe, une première symétrie saute aux yeux, en effetimplique pour une valeur donnée de
que
prend la valeur
et la valeur
ce qui donne quoi comme symétrie ?
Ensuite, il faut retenir que le sinus estpériodique on peut donc restreindre l'intervalle décrit par
à un intervalle de longueur
, prenons par exemple
et je te laisse poursuivre.
Et pouret
que valent
et
en fonction de
et
? Donc la dérivée ?
merci pour la réponse rapide
j'ai pas compris l'histoire avec la dérivée, peux-tu être plus clair dans l'explication?
intestable22 a écrit:Bonjour à tous,
j'ai un devoir à remettre pour la semaine prochaine mais je n'arrive pas à le faire.
Aidez-moi SVP si vous avez un peu de temps.
voici l'énonce:
-Dessine la courbe qui en coord. polaires a pour équation et observer les symétries éventuelles.
r²= sin2;) (sin2;) = 2sin;).cos;))
-Interprêter dx/d;) et dy/d;) et Calculer l'équation en coord. cartésienne
voila ce que j'ai trouvé pour l'équation
r²= sin2;)
r²= 2sin;).cos;)
x²+y²= 2xy / x²+y² ------> r²= x²+y³
(x²+y²)²= 2xy
x4+y4+2x²y²-2xy=0
x4+y4+2xy(xy-1)=0
je ne sais pas si c'est correct. Il me reste à tracer la courbe.
Vous pouvez me donner des pistes pour la symétrie et pour x/d;) et dy/d;).
MERCI d'avance :help:
Bonjour
il faut que sin 2;) soit positif ou nul
quand
sin(2(pi/2-;)))=sin(pi-2;))=sin(2;))
on a une symétrie par rapport à la première bissectrice
sin(2(;)+pi))=sin(2;))
on a une symétrie par rapport à l'origine
sinon, pour chaque valeur de
x= r*cos
et
y= r*sin
chan79 a écrit:Bonjour
il faut que sin 2;) soit positif ou nul
quandvarie entre 0 et pi/2, sin 2;) est bien positif
sin(2(pi/2-;)))=sin(pi-2;))=sin(2;))
on a une symétrie par rapport à la première bissectrice
sin(2(;)+pi))=sin(2;))
on a une symétrie par rapport à l'origine
sinon, pour chaque valeur de, on a
x= r*cos
et
y= r*sin
merci chan79,
ton aide ma permis d'avancer dans mon travail :lol3:
intestable22 a écrit:merci chan79,
ton aide ma permis d'avancer dans mon travail :lol3:
avec geogebra, on trace facilement cette "lemniscate"
on peut aussi taper l'équation:
(x²+y²)²=2x*y
[img][IMG]http://img571.imageshack.us/img571/4431/79068790.png[/img][/IMG]
chan79 a écrit:avec geogebra, on trace facilement cette "lemniscate"
on peut aussi taper l'équation:
(x²+y²)²=2x*y
[img][IMG]http://img571.imageshack.us/img571/4431/79068790.png[/img][/IMG]
merci pour tout,
Maintenant, il me reste qu'a interprêter dx/d;) et dy/d;).
tu peux m'aider à deriver ??
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 186 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
