Coordonnées Courbes de Bézier...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 11:32
par trablazar » 21 Fév 2012, 11:32
Salut a tous,
J'ai la un DM sur lequel je bloque un peu...
Alors voila c'est sur la courbe de Bézier ainsi que le barycentre, j'ai presque fini mais il me reste une question sur laquelle je bloque souvent: trouver des coordonnées. J'ai fait ceci sur Geogebra:
http://puu.sh/hMew ,et ,en me placant sur le repère (A;
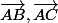
), je dois donner les coordonnées des points M,N et P.
Pour information,
le point M=A + (1 - t)

le point N=C + (1 - t)
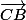
le point P=M + (1 - t)
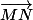
Comment suis-je censé trouver les coordonnées de ces points dans le repère (A;vecteur[A,B]vecteur[A,C]) ?
Ou peut etre que ce sont les memes coordonnées que dans le plan de base tout simplement ?
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 21 Fév 2012, 12:14
par Mortelune » 21 Fév 2012, 12:14
Oui c'est le même principe que dans le "plan de base".
Tu peux essayer d'exprimer les points en fonction de A et des vecteurs AB et AC (et de t), normalement tu pourras directement lire les coordonnées sous cette forme.
(Comme quand un point dans un plan (O,i,j) est exprimé en fonction de O, i et j)
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 12:21
par trablazar » 21 Fév 2012, 12:21
Mortelune a écrit:Oui c'est le même principe que dans le "plan de base".
Tu peux essayer d'exprimer les points en fonction de A et des vecteurs AB et AC (et de t), normalement tu pourras directement lire les coordonnées sous cette forme.
(Comme quand un point dans un plan (O,i,j) est exprimé en fonction de O, i et j)
Donc les coordonnées seraient exactement les memes ?
Enfaite ce que j'ai du mal a comprendre, c'est qu'est ce qui change entre le "plan de base" et le repère... Du moins on a l'origine A et les vecteurs AB et AC mais j'arrive pas a imaginer comment on peut exprimer des coordonnées a partir de ca
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 21 Fév 2012, 12:26
par Mortelune » 21 Fév 2012, 12:26
Non.
Si on prend le plan usuel orthonormé (O,i,j). Alors on pourra dire que A(1;1)=O+i+j.
Mais dans le plan (O,i,i+j) ce même point A sera de coordonnées (0;1).
Donc une méthode intéressante pour trouver les coordonnée dans un plan quelconque (A,u,v) c'est de trouver l'écriture d'un point M quelconque : si M=A+xu+yv alors les coordonnées de M seront (x,y).
(i,j,u & v sont des vecteurs bien sûr)
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 12:41
par trablazar » 21 Fév 2012, 12:41
Mortelune a écrit:Non.
Si on prend le plan usuel orthonormé (O,i,j). Alors on pourra dire que A(1;1)=O+i+j.
Mais dans le plan (O,i,i+j) ce même point A sera de coordonnées (0;1).
Donc une méthode intéressante pour trouver les coordonnée dans un plan quelconque (A,u,v) c'est de trouver l'écriture d'un point M quelconque : si M=A+xu+yv alors les coordonnées de M seront (x,y).
(i,j,u & v sont des vecteurs bien sûr)
Ok merci je vais chercher dans cette voie la
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 12:41
par trablazar » 21 Fév 2012, 12:41
Mortelune a écrit:Non.
Si on prend le plan usuel orthonormé (O,i,j). Alors on pourra dire que A(1;1)=O+i+j.
Mais dans le plan (O,i,i+j) ce même point A sera de coordonnées (0;1).
Donc une méthode intéressante pour trouver les coordonnée dans un plan quelconque (A,u,v) c'est de trouver l'écriture d'un point M quelconque : si M=A+xu+yv alors les coordonnées de M seront (x,y).
(i,j,u & v sont des vecteurs bien sûr)
Ok merci je vais chercher dans cette voie la.
Et donc par exemple, est-ce que M serait alors égale à 1-t ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 12:45
par chan79 » 21 Fév 2012, 12:45
salut
On sait que
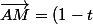\vec{AC})
on a donc les coordonnées de M
Exprime ensuite

Mais avec les barycentres, c'est beaucoup plus rapide
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 12:57
par trablazar » 21 Fév 2012, 12:57
chan79 a écrit:salut
On sait que
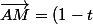\vec{AC})
on a donc les coordonnées de M
Exprime ensuite

Mais avec les barycentres, c'est beaucoup plus rapide
Deja est ce que j'ai bon en disant que M(0;1-t) ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 13:02
par chan79 » 21 Fév 2012, 13:02
trablazar a écrit:Deja est ce que j'ai bon en disant que M(0;1-t) ?
Bien-sûr, c'est ça
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 13:14
par trablazar » 21 Fév 2012, 13:14
chan79 a écrit:Bien-sûr, c'est ça
et N(2t(1-t);2t(1-t)) je vais chercher pour P mais il semble qu'il y ait a peu pres la meme relation

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 13:24
par chan79 » 21 Fév 2012, 13:24
trablazar a écrit:et N(2t(1-t);2t(1-t)) je vais chercher pour P mais il semble qu'il y ait a peu pres la meme relation
pas d'accord pour N
si tu as vu les barycentres, d'après l'énoncé
N est le barycentre de {(C,t),(B,1-t)} cela correspond à CN*=(1-t)CB*
CB* signifie vecteur CB (ça va plus vite)
C(0,1) B(1,0)
N(1-t,t)
car x(N)=(t*x(C)+(1-t)*x(B)))/(t+1-t) = t*0 +(1-t)*1=1-t
même principe pour y(N)
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 14:06
par trablazar » 21 Fév 2012, 14:06
chan79 a écrit:pas d'accord pour N
si tu as vu les barycentres, d'après l'énoncé
N est le barycentre de {(C,t),(B,1-t)} cela correspond à CN*=(1-t)CB*
CB* signifie vecteur CB (ça va plus vite)
C(0,1) B(1,0)
N(1-t,t)
car x(N)=(t*x(C)+(1-t)*x(B)))/(t+1-t) = t*0 +(1-t)*1=1-t
même principe pour y(N)
Pourrais tu me reexpliquer si tu en as le temps l'equation x(N)=(t*x(C)+(1-t)*x(B)))/(t+1-t) = t*0 +(1-t)*1=1-t ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 14:20
par chan79 » 21 Fév 2012, 14:20
trablazar a écrit:Pourrais tu me reexpliquer si tu en as le temps l'equation x(N)=(t*x(C)+(1-t)*x(B)))/(t+1-t) = t*0 +(1-t)*1=1-t ?
ce sont des formules que tu as dû voir en cours
si G est le barycentre de {(A,a) et (B,b)}
x(G)=(a*x(A)+b*x(B))/(a+b)
idem en remplaçant x par y
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 14:26
par trablazar » 21 Fév 2012, 14:26
chan79 a écrit:ce sont des formules que tu as dû voir en cours
si G est le barycentre de {(A,a) et (B,b)}
x(G)=(a*x(A)+b*x(B))/(a+b)
idem en remplaçant x par y
Ok merci cependant je ne l'ai pas encore vu on commence a peine le chapitre j'ai mentionné barycentre dans mon post parce que le prof nous a dit que ca en faisait partie merci beaucoup

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 14:38
par chan79 » 21 Fév 2012, 14:38
trablazar a écrit:Ok merci cependant je ne l'ai pas encore vu on commence a peine le chapitre j'ai mentionné barycentre dans mon post parce que le prof nous a dit que ca en faisait partie merci beaucoup
alors, il faut exprimer AN* en fonction de AB* et AC*
AN*=AC*+CN*=AC*+(1-t) CB*
et tu continues en utilisant la relation de Chasles
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 15:41
par trablazar » 21 Fév 2012, 15:41
chan79 a écrit:ce sont des formules que tu as dû voir en cours
si G est le barycentre de {(A,a) et (B,b)}
x(G)=(a*x(A)+b*x(B))/(a+b)
idem en remplaçant x par y
Je ne comprends pas dans le "idem en remplaçant x par y": dans x(G)=(a*x(A)+b*x(B))/(a+b) si je remplace avec y(G)=(A*y(a)+B*x(b))/(a+b), cela ne me donnerait-il pas le meme resultat ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 15:45
par chan79 » 21 Fév 2012, 15:45
trablazar a écrit:Je ne comprends pas dans le "idem en remplaçant x par y": dans x(G)=(a*x(A)+b*x(B))/(a+b) si je remplace avec y(G)=(A*y(a)+B*x(b))/(a+b), cela ne me donnerait-il pas le meme resultat ?
si tu n'as pas vu les barycentres, tu ne peux pas faire comme ça
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 15:55
par trablazar » 21 Fév 2012, 15:55
chan79 a écrit:si tu n'as pas vu les barycentres, tu ne peux pas faire comme ça
Mais puisque j'ai les coordonnées de M et N, ne puis je pas appliquer la méthode que tu as utilisé pour trouver N ? Du moins (je pense) si P est le barycentre de MN ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Fév 2012, 16:11
par chan79 » 21 Fév 2012, 16:11
trablazar a écrit:Mais puisque j'ai les coordonnées de M et N, ne puis je pas appliquer la méthode que tu as utilisé pour trouver N ? Du moins (je pense) si P est le barycentre de MN ?
Si
P((1-t)²,2t-2t²)
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 21 Fév 2012, 16:40
par trablazar » 21 Fév 2012, 16:40
chan79 a écrit:Si
P((1-t)²,2t-2t²)
Ok mais je pense qu'il faudra que je demande a mon prof de m'expliquer avec détails...
Pourrais tu m'aider ( j'en demande un peu trop mais la c'est incomprehensible pour moi ) pour ce qui est d'exprimer AP* en fonction de AB* et de AC* ? Je pensais faire AP=AB+BP ou AP=AC+CP Mais étant donné qu'il faut l'exprimer en fonction des deux je pensais faire AP=((AB+BP)+(AC+CP))/2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 181 invités
