Convergence des suite 1/n ; 1/n² ; 1/racine carrée de n

[Tulipe06]

Bonjour,

Qui peut m'expliquer la démonstration de la convergence vers 0 des suites: 1/n ; 1/n² et 1/ ?
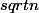
Pour démontrer que 1/n converge vers 0, on choisit un intervalle ouvert, centré en 0, soit A = -a;a (intervalle ouvert des 2 côtés). Avec a>0.
Pourquoi a t-on n>1/a?
La démonstration est: pour tout n>1/a on a 0 1/a?

Et comment démontrer la convergence de ?

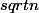
D'avance merci pour vos réponses.

[MouLou]

Bonjour,

Qui peut m'expliquer la démonstration de la convergence vers 0 des suites: 1/n ; 1/n² et 1/ ?
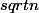
Pour démontrer que 1/n converge vers 0, on choisit un intervalle ouvert, centré en 0, soit A = -a;a (intervalle ouvert des 2 côtés). Avec a>0.
Pourquoi a t-on n>1/a?
La démonstration est: pour tout n>1/a on a 0 1/a?

Et comment démontrer la convergence de ?

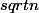
D'avance merci pour vos réponses.

Bah ca dit tout simplement que si tu te fixes a, donc tu fixes un nombre 1/a, tu vas pouvoir trouver un entier supérieur a 1/a, par exemple partie entière de 1/a+1. C'est toi qui choisit les n tels que ca marche

[Tulipe06]

Bah ca dit tout simplement que si tu te fixes a, donc tu fixes un nombre 1/a, tu vas pouvoir trouver un entier supérieur a 1/a, par exemple partie entière de 1/a+1. C'est toi qui choisit les n tels que ca marche

Merci pour ta rapidité. Si je comprends bien, je choisis n comme ça m'arrange???
Et si n <1/a alors la suite 1/n ne converge pas vers 0?

[Tulipe06]

Merci pour ta rapidité. Si je comprends bien, je choisis n comme ça m'arrange???
Et si n <1/a alors la suite 1/n ne converge pas vers 0?

Personne pour m'éclairer???

[chan79]

Personne pour m'éclairer???

Pour montrer que 1/n a comme limite 0, il faut montrer qu'on peut le rendre aussi petit que n'importe quel nombre A à partir d'un certain rang.
Autrement dit, A étant donné il faut trouver N tel que si n>N alors 1/n1/A alors 1/n <A

Par exemple, si on veut que 1/n<0.001, il suffit que n soit plus grand que 1/0.001 soit 1000