Racine carrée suite

[denis273]

quelqu'un aurait une idée de la méthode à suivre pour montrer que \/¯((8^10+4^10)/(8^4+4^11))= 16\/¯((2^10+1)/1+4^5)). cordialement denis

[johnjohnjohn]

quelqu'un aurait une idée de la méthode à suivre pour montrer que \/¯((8^10+4^10)/(8^4+4^11))= 16\/¯((2^10+1)/1+4^5)). cordialement denis

8 = 2 * ?

Factorise autant que faire ce peut ce qu'il y a dans les parenthèses

[denis273]

\/¯((2^3)^10+(2^2)10)/((2^3)^4+(2^2)^11) = \/¯(2^30+2^20)/(2^12+2^22) et par la suite ?

[johnjohnjohn]

\/¯((2^3)^10+(2^2)10)/((2^3)^4+(2^2)^11) = \/¯(2^30+2^20)/(2^12+2^22) et par la suite ?

Tu as développé. Il faut factoriser !

Prenons un de tes termes :

(2^3)^10+(2^2)10=(2^2)^10*(2^10 +1 )

[denis273]

je n'ai pas tout suivi à votre factorisation , on passe d'une addition de 2 termes à une multiplication , vous pouvez m'expliquer un peu plus silvouplait ?

[denis273]

excusez moi je suis aller un peu vite , non c'est bon j'ai suivi , je vais continuer et je vous montre cela

[denis273]

j'ai essayer de grater quelquechose mais je suis vraiment en panne sur le dénominateur pour obtenir ...(1+4^5)
8^4+4^11=2*(4^4)+4^11= ? ? ?

[johnjohnjohn]

j'ai essayer de grater quelquechose mais je suis vraiment en panne sur le dénominateur pour obtenir ...(1+4^5)
8^4+4^11=2*(4^4)+4^11= ? ? ?

8^4+4^11=(4*2)^4+ 4^11=4^4(2^4+4^7)=.....

Faut aussi remarquer que 4=2*2 :zen:

[Ben314]

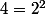
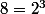
A mon avis, le plus simple est tout de même de constater que et que , ce qui permet de n'avoir que des puissances de deux :

Procède de même pour l'autre coté.

[denis273]

merci beaucoup pour votre aide , en effet la solution de ben est plus facile mais merci à vous 2