bonjour
je suis coincée à cette exercices est ce que vous pourriez m'aidez merci
https://fromsmash.com/mathiage
√(2√(2√(2√(√2) ) ) ) converge t-elle
11 messages
- Page 1 sur 1
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
Bonjour,
on pose=\sqrt{2x}) . La fonction f est elle croissante ? décroissante ?
. La fonction f est elle croissante ? décroissante ?
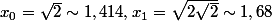
Qu'est ce que l'on peut en déduire pour la suite) ?
?
quels sont les points fixes de f ,i.e, les racines de l'équation x=f(x) ?
f admet comme points fixes 0 et 2. Montrer que la suite (x_n) est majorée par 2.
En déduire que la suite est convergente et que sa limite est 2 quand tend vers l'infini.
on pose
Qu'est ce que l'on peut en déduire pour la suite
quels sont les points fixes de f ,i.e, les racines de l'équation x=f(x) ?
f admet comme points fixes 0 et 2. Montrer que la suite (x_n) est majorée par 2.
En déduire que la suite est convergente et que sa limite est 2 quand tend vers l'infini.
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
Merci grâce à toi je pense avoir réussi
mais est ce que tu pourrais voir ci c'est cela Merci
https://fromsmash.com/image23456
mais est ce que tu pourrais voir ci c'est cela Merci
https://fromsmash.com/image23456
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
Bonjour,
il y a de bons éléments mais cela manque de précision par endroit.
Il faut
1) montrer que la fonction est croissante (ok, mais peut sans doute s'argumenter sans calculer la dérivée)
2) montrer que la suite est croissante (argumentation au mieux peu claire, le mieux est de procéder par récurrence)
3) montrer que la suite est majorée (pas fait, se fait aisément par récurrence)
4) en déduire que la suite converge
5) calculer les limites possibles et en déduire la limite de la suite
il y a de bons éléments mais cela manque de précision par endroit.
Il faut
1) montrer que la fonction est croissante (ok, mais peut sans doute s'argumenter sans calculer la dérivée)
2) montrer que la suite est croissante (argumentation au mieux peu claire, le mieux est de procéder par récurrence)
3) montrer que la suite est majorée (pas fait, se fait aisément par récurrence)
4) en déduire que la suite converge
5) calculer les limites possibles et en déduire la limite de la suite
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
pour tout entier n,
)
la fonction f est strictement croissante sur (comme composée de deux fonctions strictement croissantes) et envoie
(comme composée de deux fonctions strictement croissantes) et envoie  sur
sur 
démo de la croissance de la suite) :
:
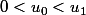
on fait l'hypothèse de récurrence:
n entier 1 ,
1 ,  : 0 < u_{n-1} < u_ {n})
on compose par f:
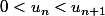
donc) est héréditaire.
est héréditaire.
Comme elle est initialisée à n=1, elle est donc vraie pour tout entier
la fonction f est strictement croissante sur
démo de la croissance de la suite
on fait l'hypothèse de récurrence:
n entier
on compose par f:
donc
Comme elle est initialisée à n=1, elle est donc vraie pour tout entier
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
démo de la majoration de (u_n):
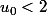
on fait l'hypothèse de récurrence
 : u_n < 2)
en composant par f:
)

Donc) est héréditaire et initialisée pour n=0. Elle est donc vraie quel que soit n .
est héréditaire et initialisée pour n=0. Elle est donc vraie quel que soit n .
donc) est majorée par 2.
est majorée par 2.
on fait l'hypothèse de récurrence
en composant par f:
Donc
donc
Modifié en dernier par mathelot le 28 Oct 2022, 13:49, modifié 1 fois.
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
LZIN a écrit:Merci
est ce que c'était juste le seul problème
non, il y a la majoration de la suite et la démo que sa limite est 2.
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
La suite) est croissante, majorée, elle converge vers une limite l strictement positive.
est croissante, majorée, elle converge vers une limite l strictement positive.
on a:
)
La fonction f étant continue sur R+*, on a:
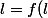)
donc la limite l vaut 0 ou 2.
Comme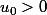 , la limite de la suite
, la limite de la suite  ) est 2.
) est 2.
on a:
La fonction f étant continue sur R+*, on a:
donc la limite l vaut 0 ou 2.
Comme
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
LZIN a écrit:Merci
est ce que c'était juste le seul problèmes
Je pense que globalement, il te manquait deux démonstrations par récurrence.
Si tu es en Terminale, c'est au programme. Si tu es en classe de Première, c'est plus délicat.
Re: √(2√(2√(2√(√2) ) ) ) converge t-elle
Merci beacoup
je vais appliquer tes conseils et je suis en terminal
je vais appliquer tes conseils et je suis en terminal
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
