Continuité de la fonction lxl

[fpaco]

Bonjour,
J'aimerai juste avoir votre avis sur ma démonstration pour montrer que la fonction valeur absolue est continue en tout point, juste savoir si le raisonnement est correcte.

Soit ll définie sur
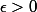
Soit . On pose tel que , ll .
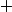
On a ll = l l ll ll
Donc ll ll ll
De même que ll ll ll ll
Ainsi l llll l ll
On peut donc conclure que lll
Donc on a ll =
Ainsi la fonction valeur absolue est continue en tout point réel.

Merci de vos réponses

[mathelot]

Le raisonnement est correct.
x0 réel.
Pour tout epsilon reel strictement positif, il existe alpha reel Strictement positif tel que
Pour tout x réel (|x-x0|<alpha implique |f(x)-f(x0) | <epsilon)

[fpaco]

Ok merci beaucoup