Construire point

[posso49]

jj.jpg

Bonjour. Je cherche de l'aide pour la 2eme question de cet exercice.
Soit un cercle O, un diamêtre XY, deux points A et B sur un des demi-cercles limités par XY et un point C sur l'autre. CA et CB coupent XY en P et Q tels que OP=OQ.
1) Soit B' le point diamétralement opposé à B. Que peut-on dire du quadrilatère BPB'Q? Comparer les angles B'PC et ACB.
Comme on a OP=OQ et OB=OB', le quadrilatère BPB'Q, qui a ses diagonales qui se coupent en leur milieu est un parallélogramme. PB'//QC => B'PC=ACB comme angles alternes internes.
2)Les points A et B étant donnés ainsi que le diamètre XY, construire le point C de façon que OP = OQ.
A part construire le point B', je ne sais pas comment faire pour positionner P et Q.
Merci pour votre aide.

[Ben314]

Salut,
Ca m'a fait pas mal cogiter ton truc et la seule solution que j'ai risque d'être "hors de portée" si tu n'a pas vu la notion dite d'arc capable.

Capture.png (48.58 Kio) Vu 490 fois

L'angle c'est la moitié de l'angle au centre 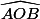que tu connait sans même avoir construit le point .
Ensuite, tu cherche le point tel que l'angle soit égal à ce qui signife qu'il est situé sur l'arc capable passant par et 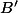d'angle .
On montre ensuite (relativement) aisément que cet arc est porté par le cercle de centre qui est l'intersection des tangentes en et en 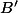au cercle de départ.
Le point est donc l'intersection du segment et du cercle centré en passant par (et 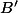). (et évidement on construit ensuite facilement puis )

La construction est en soi extrêmement simple (deux perpendiculaires puis un cercle à tracer), mais la justification demande pas mal de connaissances.
Peut-être que quelqu'un trouvera plus simple...

[siger]

bonsoir

sauf erreur

tracer AB' et considerer les angles interceptant le meme arc sur le cercle
1- B'AC = B'BC. ( arc B'C)
2- dans le triangle isocele AB'P : B'AP = AB'P
3- PB'O = B'BC ( alterne- interne)
4- AB'B = ACB = AOB /2 ( arc AB)
donc B'BC = AOB /4

a pres mesure de l'angle AOB on trace, a partir de B, une droite faisant un angle AOB /4 avec BO qui coupe le cercle en C

[Ben314]

2- dans le triangle isocele AB'P : B'AP = AB'P

Je pense que non :

Capture.png (42.96 Kio) Vu 468 fois

[siger]

re

OK: AB'P n'est pas isocele dans le cas general
(mauvaise lecture d'un dessin a main levée, tout a fait inexcusable)
Merci Ben314

contribution a oubliier

[posso49]

Merci à vous deux pour vos réponses. Je connais l'arc capable Ben. Je cherchais à en construire un mais je ne voyais pas lequel. Merci et bon week-end.

[Ben314]

Si ça peut te rassurer, ça m'a pas du tout sauté aux yeux non plus et je vais essayer de le garder dans mes "anales" de casse tête "assez trapu" : Sans les indications préliminaires (construire le symétrique B' de B et montrer que les angles B'PC et ACB sont égaux), ça me semble bien "casse tête" de trouver une construction simple du point C.

Si je suis pas indiscret, c'est tiré d'où comme exercice ? (mon petit doigt me suggère que ça provient pas d'un bouquin récent d'enseignement...)

[siger]

re

malgré de nombreuses cogitations je n'ai pas trouvé plus simple....comme suggéré par Ben314!
si tu as une correction (ou une autre deonstration) quelque part je suis preneur de la solution ...pour mon info personnelle
merci

[posso49]

C'est tiré de Lebossé-Hémery 1965. Ce n'est pas récent, c'est vrai. Il y a quelques exercices difficiles. Je suis en train de les reprendre. Cordialement.

[Pseuda]

Bonsoir,

J'ai essayé avec les parallèles et la symétrie de centre O. On y arrive en construisant plusieurs parallélogrammes successivement, mais c'est moins simple qu'avec le théorème de l'angle inscrit (ou arc capable) étendu à la tangente au cercle.

Petite variante : j'ai construit par l'intersection de la tangente en B' au cercle de centre O, et la médiatrice de [AB'].

[Ben314]

Si c'est ce bouquin là :
https://manuelsanciens.blogspot.fr/2012 ... se-de.html
Et que l'exercice provient de la Leçon 2 : Angles orientés dans le plan (ce qui semblerais logique)

Alors je me demande ce que ça va être une fois arrivé à la Leçon 11 : Division et faisceau harmoniques ; Polaire d’un point par rapport à deux droites. . .

Et si j'ai bien compris c'est un bouquin de Terminale. . .

(re)Question : c'est une version papier que tu as ou bien y-a-t-il un endroit où on peut le trouver sous forme numérisé ?

[annick]

Ah ! Que de souvenirs dans le Lebossé Hémery. J'ai toujours le mien qui date de 1967, programme de 1966. Il est plein d'annotations et est resté mon livre de référence pour étayer les cours particuliers de maths que j'ai donnés pendant plus de 30 ans.

[Ben314]

Ah, là on sent qu'on est pas de la même génération : Moi, mon bouquin de Terminale de "géométrie" (1983), il commençait par :
Chapitre I : (Révisions) Groupes, Anneaux, Corps, Espaces vectoriels...

[Pseuda]

Tout ça (le contenu de ce Lebossé, Hémery, dont j'avais déjà entendu parler), était au programme du Capes dans les années 90. Les maths changent peu finalement, ce sont les programmes qui évoluent, et la façon d'aborder les choses.

Par exemple, l'angle de 2 droites a disparu des programmes. Mais il y aurait tellement de choses à voir, il faut bien faire un choix.

[posso49]

Cet exercice est un exercice de révision du programme de 2°C. Je ne suis pas encore arrivé au programme de terminale et j'aurai probablement l'occasion de reposter d'autres exercices.
J'ai acheté la collection sur Internet il y a 3 ans. Il y en a encore quelques uns en vente de temps en temps.