X^2+x+11 congrue à 0 modulo 143 résoudre dans Z

[HUGOMATHEMATIQUES]

Hello tout le monde, Merci d'avance pour votre aide.
Voici mon problème je dois résoudre le modulo suivant : Résoudre dans Z l’équation x^2+x+11≡0[143].
J'ai déjà pas mal plancher sur la question, et une disjonction de cas semble évidemment impossible.
Je pensais trouver avec x1≡x2[143] ce qui induit que x1^2+x1+11≡x2^2+x2+11[143]. Mais je suis bloqué. Quelqu'un aurait une piste pour résoudre le modulo ??
Merci d'avance,
Bonne soirée

[GaBuZoMeu]

Bonsoir,
Oh, une équation du second degré ! Je me précipite sur le discriminant, et je constate facilement qu'il est congru modulo 143 à un carré parfait sympathique !

[HUGOMATHEMATIQUES]

Salut Gabuzomeu, Merci beaucoup de ta réponse !! Si j'ai bien compris ta réponse, j'obtient le discriminant delta≡100[143]. 100 est bien le carré parfait de 10, mais je ne vois pas ce que cela induit. J'ai pas mal chercher sur internet ce qu'un carré parfait dans un modulo induit mais n'ai pas trouvé. Aurais tu d'autres conseils ?
Merci d'avance d'avoir pris le temps de t'intéressé à ma question.
Bonne journée et bonne fin de week-end

[catamat]

Bonjour

Le principe reste le même les formules de x' et x" restent valables mais elles ont été obtenues dans un corps par la propriété un produit est nul ssi l'un des facteurs est nul.
Or ici ce n'est pas un corps, si l'on calcule 11*13 cela donne 0 donc on n'a pas toutes les solutions en utilisant la méthode classique.
Mais bien sûr elles sont quand même solutions puisque en multipliant par 0 dans Z/143Z on obtient 0.

Pour obtenir les valeurs facilement le -b qui vaut -1 pourra être remplacé par 142.

Mais il y a d'autres solution 11 en est une pratiquement évidente...

Pour obtenir ces autres solutions on pourra utiliser la forme canonique, écrire l'équation sous la forme (x+d)²=e et chercher les nombres dont les carrés valent e modulo 143.

[GaBuZoMeu]

La méthode habituelle nous donne des entiers et tels que, pour tout entier , est congru à . Après bien sûr il reste à voir quels sont les entiers tels que divise .

[mathsnnn]

Bonjour catamat,
je trouve bien avec cette méthode que (x-71)^2=5^2[143] mais je suis bloqué,
pourrais tu m'aider stp ?
Merci par avance, bonne fin de week end

[GaBuZoMeu]

Bravo, tu as déjà comme ça deux des quatre solutions modulo 143., appelons les et , et une factorisation de en modulo 143.
Il te reste à voir quels sont les tels que divise . Il y a bien sûr et modulo 143, mais il y en a deux autres.

[mathsnnn]

(x-76)(x-66)=0[143]
Avec ceci on voit comme tu l'as dit que x=76[143] et x=66[143] son des racines évidentes. Mais honnêtement, je ne vois pas comment obtenir les deux autres et surtout à justifier correctement qu'il n'y en a que deux autres.

[GaBuZoMeu]

Comment est-ce que le produit de deux nombres peut être divisible par ? L'un des deux peut être divisible par . Si ce n'est pas le cas, l'un peut être divisible par 11 et l'autre par 13.

[mathsnnn]

Oui et cela me donne deux systèmes : {x=10[11] et x=1[13]} ou {x=0[11] et x=11[13]}. Je résous des équations diophantiennes et j'ai l'impression de me perdre d'autant plus que les résultats que je trouve sont faux.

[GaBuZoMeu]

Oui, tu as bien identifié les deux systèmes de congruences qui vont donner les deux autres solutions modulo 143. Résoudre des systèmes de congruence avec des modules premiers entre eux, c'est l'agorithme du théorème des restes chinois qui fait intervenir une identité de Bézout entre les modules. Tout ce qu'il y a de plus classique, mais il faut l'avoir vu. L'as-tu vu ?

PS. J'ajoute que le deuxième système est particulièrement simple à résoudre, tu cherche un nombre (modulo 143) qui est divisible par 11 et congru à 11 modulo 13.
Et à partir du moment où tu as celui-ci, appelons-le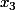 , tu sais (peut-être) que va se factoriser modulo 143 en .

[mathsnnn]

Merci beaucoup. Je ne connais pas ce théorème et ai donc utilisé l'autre astuce que tu donnes. Pour le système simple à résoudre on obtient x=11[143] donc (x-11)(x-y)=x^2+x+11[143] (y étant la dernière racine que l'on cherche). mais par identification j'ai x=-12[143] et x=1[143] ce qui est impossible, je ne comprends pas.

[GaBuZoMeu]

Si est congru à modulo 143, alors 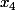est congru à 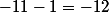ou encore 131 modulo 143. Et tu peux vérifier que est bien congru à 11.
D'où sors-tu ce 1 modulo 143 ?

[mathsnnn]

excuse moi j'ai vu mon erreur je suis allé trop vite.
Merci beaucoup pour tous ces conseils, bonne soirée.

[GaBuZoMeu]

Avec plaisir.