Comment montrer que x²+y²+xy=1 implique x^3y + y^3x < 2

[AnassBkm]

Svp j'ai besoin d'un aide je suis dans une classe sience math 2année lycée et notre prof nous a donné cet exercice ci dessous:
Comment montrer que x²+y²+xy=1
x^3y + y^3x < 2
Merci d'avance

[chan79]

salut
factorise xy dans la seconde expression

[AnassBkm]

salut
factorise xy dans la seconde expression

Bonsoir,
ça me donne xy(x²+y²) inférieur à 2
et puis? je ne sais pas comment continuer

j'ai un autre idée,
x²+y²=1-xy
on sait que x²+y² est toujours positive ou nul
donc 1-xy 0
d'ou 1 xy
et puisque xy est inférieur à 1
donc soit x 1 et y 1 et vis versa
soit les deux 1..

je me suis bloqué une autre fois..

[Ben314]

Salut,
A mon avis, ce que préconisait chang79, c'est de dire que, vu que x²+y²+xy=1, on a
xy(x²+y²) = [1-(x²+y²)](x²+y²) = (1-t)t où t=x²+y²
et là, on peut songer à étudier la fonction (1-t)t sur R+ pour trouver son maximum (ou bien mettre ce trinôme sous forme canonique si on a pas vu les études de fonction)

[chan79]

j'avais pensé à presque la même chose:

x³y+xy³=xy(x²+y²)=xy(1-xy)
si on pose t=xy, il faut montrer t(1-t)<2 soit t²-t+2>0

[Lostounet]

j'avais pensé à presque la même chose:

x³y+xy³=xy(x²+y²)=xy(1-xy)
si on pose t=xy, il faut montrer t(1-t)<2 soit t²-t+2>0

Dsl j'ai supprimé mon message car j'avais fait une hypothèse peu intelligente.

Mais en effet j'avais bien mis xy(x^2 + y^2) = xy(1 - xy) et fallait majorer cette choses sans commettre une grosse bêtise

Edit: En plus Ben a déjà écrit la même chose
Il faut que je me déconnecte et que j'aille boire un verre

[Razes]

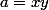
On pose et (donc )



il faut montrer

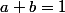
Résumé: et ; montrer

Utiliser: