On a a et b supérieur strictement à 0
En utilisant l'inégalité de cauchy shwartz monter que
(a+b)(1/a +1/b) >= 4
Cauchy schwarz
5 messages
- Page 1 sur 1
Re: Cauchy schwarz
Bonsoir
(CS).On peut prouver la plupart des inégalités grâce à elle!
Ici ce n 'est pas compliqué d 'autant plus que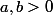
donc en utilisant : \left( { { { b }^{ 2 } }_{ 1 }+{ b^{ 2 } }_{ 2 }+... } \right) \ge \left( { a }_{ 1 }{ b }_{ 1 }+{ a }_{ 2 }{ b }_{ 2 }+.. \right)^2)
donc....
(CS).On peut prouver la plupart des inégalités grâce à elle!
Ici ce n 'est pas compliqué d 'autant plus que
donc en utilisant :
donc....
Re: Cauchy schwarz
Soit deux vecteurs u et v, Cauchy-Schwartz dit que <u,v> <= ||u||.||v||. Re-écris cette inégalité avec les coordonnées de u et v... trouve ensuite les bonnes coordonnées de u et v pour que cela donne (a+b)(1/a +1/b)<=4
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
