Calcul somme termes de une suite

[Olivierlacanau]

Bonjour,
Je souhaiterais calculer la somme des termes de la suite T(n) = p + n² lorsque par exemple p=11, 1er terme de la suite et 36 le dernier.
En résumé, quelle formule pour calculer la somme des termes suivants 11-12-15-20-27-36 (121)
Je ne comprends pas pourquoi la formule (nbre termes×(1er terme+dernier terme))/2 ne fonctionne pas...141 au lieu de 121
En vous remerciant par avance,
Cordialement
Olivier

[catamat]

Bonjour,
La formule que tu cites est valable pour les suites arithmétiques, or ici ce n'est pas uns suite arithmétique.

Dans ce cas il faut connaître la formule de la somme des carrés de 1 à n² :
http://villemin.gerard.free.fr/Wwwgvmm/ ... mCarre.htm

[Olivierlacanau]

Merci bien. Je vais jeter un oeil.

[Olivierlacanau]

C bon je crois avoir trouvé :
La formule est donc la suivante pour p=11
1/3((p-1)/2)^3+1/2((p-1)/2)^2+1/6((p-1)/2+((p+1)/2)*p
125/3+25/2+5/6+6*11=121
= 11+12+15+20+27+36
Est-ce correct ?
Par avance merci

[Olivierlacanau]

Bon ça a l air de marcher pour tous les nombres.
P=7
9+9/2+3/6+8/2×7 = 42
7+8+11+16 = 42
Merci Catamat.
Maintenant je souhaiterais extraire la somme des valeurs paires d un côté et des valeurs impaires de l autre...(pour une bonne raison...)
Par exemple, pour p=7
D un côté : 7+11 = 18
De l autre : 8+16 = 24
Comment puis-je m y prendre ?
Par avance merci

[mathelot]

bonsoir,



on calcule le terme de gauche de l'égalité et le terme le plus à droite en factorisant par 4.

[Olivierlacanau]

Bonsoir Mathelot,
Je te remercie pour ta réponse mais je n' ai malheureusement pas le niveau en mathématiques pour appréhender à sa juste valeur la pertinence de ta réponse.
A quoi correspond cette égalité ?
En fait, je recherche juste une formule qui me permettrait en l intégrant dans un tableur de calculer les nombres pairs (ou impairs) de la suite T(n) = p + n² comme je l ai fait précédemment et avec l aide de Catamath, l intégralité des termes de cette suite entre p et (((p+1)/2)^2.
Je ne sais si je m exprime clairement...
Désolé...
Merci

[catamat]

Bonjour

Les sigma te semblent peut-être compliqués... ce que veut dire la formule de Mathelot c'est que la somme des termes de rangs impairs + la somme des termes de rangs pairs est égale à la somme de tous les termes de la suite.

Encore plus simplement

1²+2²+3²+4²+5²+6²+7²+8² = (1²+3²+5²+7²)+(2²+4²+6²+8²)
le second membre pouvant s'écrire :
=(1²+3²+5²+7²)+ 4(1²+2²+3²+4²)

car pour les nombres pairs, on a : (2k)²=2²k²=4k²

On peut alors calculer (avec la formule) le membre de gauche 1²+2²+3²+4²+5²+6²+7²+8² et la deuxième parenthèse de celui de droite 1²+2²+3²+4²,
l'égalité permet alors de trouver la première parenthèse 1²+3²+5²+7².

[Olivierlacanau]

Super, à présent c limpide. Merci beaucoup pour votre patience et votre pédagogie.

[Olivierlacanau]

Muum je me suis peut-être réjoui un petit peu trop vite !
J'ai compris que pour obtenir la somme de tous les termes de la suite T(n) = p + n² avec par exemple p=7, il suffit de poser :
1^2+2^2+3^2 + ((7+1)/2)
G bien saisi la formule 1/3n3+1/2n2+1/6n pour calculer la première partie de cette expression.
G également bien compris la méthode pour calculer la somme des termes pairs et impairs de cette même partie de l'expression : (1^2+3^2) + (2^2) -4*(1^2)
Impairs = 10 et pairs =4
Par contre, je ne sais pas quoi faire de la seconde partie de l'expression qui m'intéresse 1^2+2^2+3^2 + ((7+1)/2) pour procéder à l'"extraction" des pairs et des impairs...pfff, c'est navrant !
Par avance, je vous remercie !

[Olivierlacanau]

Pour préciser ma deuxième phrase :
"J'ai compris que pour obtenir la somme de tous les termes de la suite T(n) = p + n²" jusqu'au terme ((p+1)/2)^2.

[Olivierlacanau]

Oh zut, me suis encore trompé ! La bonne expression : 1^2+2^2+3^2 + ((7+1)/2)*p

[catamat]

Bon je dois dire que j'ai du mal à vous suivre dans vos différents changements de formule ...

Un problème que l'on n'a pas vraiment évoqué c'est le terme constant p.
Bien sûr si on l'ajoute x fois on a une somme égale à xp.

Avant de me lancer dans une explication détaillée pouvez vous me dire exactement ce que vous devez calculer.

[Olivierlacanau]

Je vais essayer d'être plus clair :
A la base, je souhaitais calculer la somme des termes de la suite T(n) = p + n² de p jusqu'à ((p+1)/2)^2.
Grâce à vos explications et en me rapportant à la page de Gérard Villemin , j'ai réussi à trouver la formule qui me permet d'y arriver :1/3((p-1)/2)^3+1/2((p-1)/2)^2+1/6((p-1)/2+((p+1)/2)*p.
Cette formule a pour équivalence 1^2+2^2+3^2...((p-1)/2)^2 +((p+1)/2)*p.
A présent, j'aurais voulu calculer la somme des termes pairs de cette somme et puis par soustraction la somme des termes impairs.
Vous et matelot, m'avez expliqué comment le faire pour la première partie de la précédente formule 1^2+2^2+3^2...((p-1)/2)^2 mais cela se complique pour moi lorsque, je prends en considération la formule dans son intégralité 1^2+2^2+3^2...((p-1)/2)^2 +((p+1)/2)*p.
En résumé, quelle est la formule qui me permette, en l'intégrant dans un tableur, de calculer la somme des termes pairs de la suite, par exemple, T(n) = 7 + n² de p jusqu'à ((p+1)/2)^2. (16) sachant que je sais déjà calculer la somme de l'intégralité des termes ?
Pour reprendre l'exemple p=7
La liste des termes est 7-8-11-16. Je sais à présent calculer leur somme totale (42) mais pas spécifiquement la somme des nombres pairs (24). Vous m'avez expliqué qu'il fallait d'abord calculer la somme des pairs pour pouvoir ensuite déterminer par soustraction celle des impairs mais en prenant pour exemple ce que j'appelle la première partie de ma formule (en gras)1^2+2^2+3^2...((p-1)/2)^2 +((p+1)/2)*p.
Or, je n'arrive pas à adapter votre méthode à la formule complète...
Pfff, je ne sais pas si c'est beaucoup plus clair...
En vous remerciant pour votre indulgence...

[catamat]

Bon ok je pense avoir compris ...

En fait p est un nombre impair, donc p=2k+1 avec k entier.

On y ajoute les carrés successifs jusqu'à celui de k on a alors 2k+1+k² qui est égal à (k+1)² qui est le dernier terme de votre somme.

On peut donc l'écrire


Comme vous le voyez j'ai séparé la partie constante (2k+1) et la partie variable i².

Si vous voulez l'exprimer en fonction de p il suffit de remplacer k par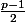 , on obtient :

S=

En prenant p=7 on trouve 42
pour p=11 on trouve 121 comme prévu

Voilà pour la formule générale.
Si on est ok je vous parlerais de la somme des termes impairs

[Olivierlacanau]

Vos explications sont limpides.
Votre formule est beaucoup plus digeste que la mienne.
J ai bien compris votre raisonnement.
Je suis prêt pour la suite !

[catamat]

Ok la suite c'est un peu plus technique....

Cela dépend d'abord du nombre total de termes qui est k+1.
Dans un premier temps je vais supposer k PAIR.

Si k est pair, on aura un nombre impair de termes.
Or le premier est impair et le dernier impair car c'est (k+1)² , donc on a plus d'impairs que de pairs.

Si on a k=2n avec n entier, on aura n termes pairs et n+1 termes impairs pour un total qui est bien de 2n+1 termes (ou k+1 termes).

J'ai compris que seule la somme des impairs vous intéresse, or les termes impairs sont obtenu lorsque i est pair car alors i² est pair et p+i² impair (puisque p est impair)

Pour avoir i pair je le remplace par 2j , avec j variant de 0 à n, 2j prend alors les valeurs 0, 2, 4,... 2n soit les n+1 termes impairs.

Bien sûr k a été remplacé par 2n. Voilà la somme à calculer :



Or (2j)²=4j² donc



Donc

Ex : pour p=9 on a k=4 qui est pair et donc n=2
La somme est
9+10+13+18+25

La somme des impairs 9+13+25=47
La formule donne le même résultat.

Si vous la voulez en fonction de p je vous laisse calculer il faut remplacer n par k/2 et k par (p-1)/2.

Pour le cas , k impair essayer de le résoudre je vous dirai si c'est bon.

[Olivierlacanau]

Encore une fois merci beaucoup.
Je me penche sur le pb dès que possible et je reviens vers vous.
Je ne fais cela qu à titre de loisir... J ai malheureusement d autres obligations professionnelles...
Merci encore!
Cordialement