Calcul de module et argument avec tanx (TS)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lisandro
- Messages: 3
- Enregistré le: 12 Jan 2010, 13:44
-
 par Lisandro » 03 Mar 2010, 18:45
par Lisandro » 03 Mar 2010, 18:45
Bonjour,
Pour la résolution d'une éqution je dois calculer le module et l'argument de:
tan(x)+i
et
tan(x)-i
Avec 0;)x<(pi/2)
Mais je n'a arrive pas à déterminer un résultat, exploitable, pouvez vous m'aider.
Merci.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Mar 2010, 18:50
par Sylviel » 03 Mar 2010, 18:50
comment s'écrit tan en fonction de sin et cos ? Comment s'écrit un complexe en fonction de son module et de son argument ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 03 Mar 2010, 18:52
par annick » 03 Mar 2010, 18:52
Bonjour,
Tu poses r(cos t+isint)=tanx+i
Et tu égalises les réels et les imaginaires.Tu n'oublies pas que tanx=(sinx/cosx) et que sin²x+cos²x=1 et tu verras, tout s'arrange un peu
-
Lisandro
- Messages: 3
- Enregistré le: 12 Jan 2010, 13:44
-
 par Lisandro » 03 Mar 2010, 19:10
par Lisandro » 03 Mar 2010, 19:10
Merci pour votre aide je vais essayer et vous tenir au courant
-
mathelot
 par mathelot » 03 Mar 2010, 19:27
par mathelot » 03 Mar 2010, 19:27
Bj,
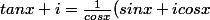 = \frac{ie^{- ix}}{cosx})
d'où la forme trigo
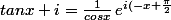})
en conjuguant
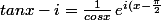})
de module
^{-1})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
