Je voulais savoir si je pouvais vous soumettre une correction à un exercice de calcul matriciel !
Merci d'avance !
Voici le sujet et mes travaux :

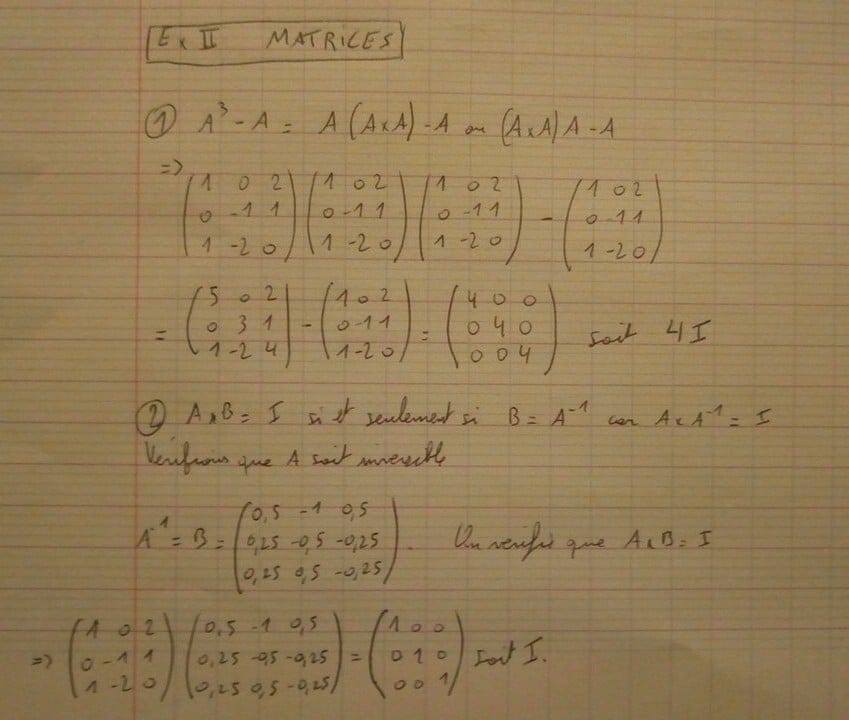

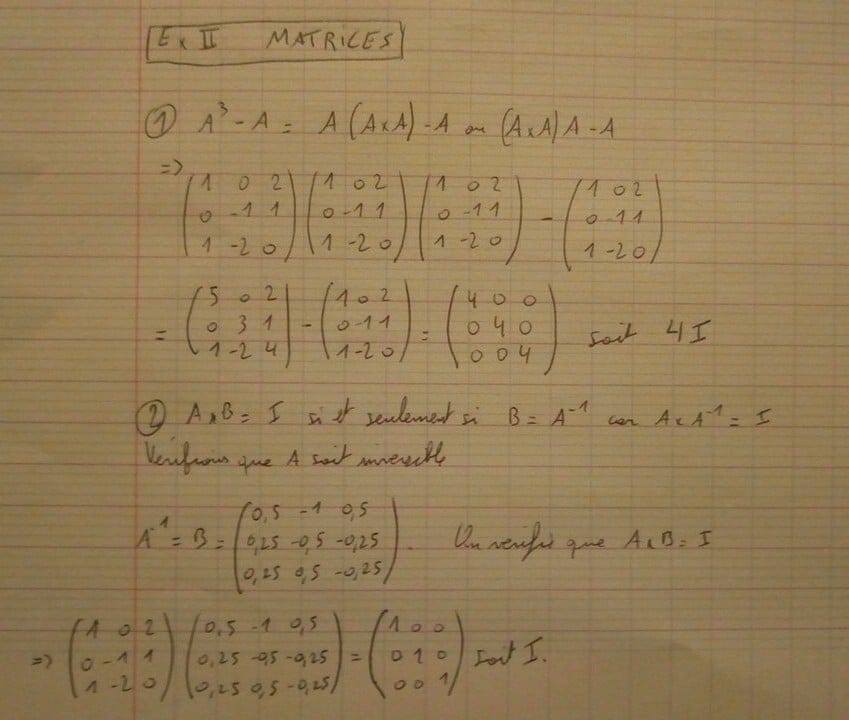
pascal16 a écrit:de plus A et A commutent, donc c'est l'inverse à gauche et à droite de A, ie AB=BA=Id
aviateur a écrit:Un bon petit exo d'algèbre intéressant serait de démontrer que si AB=I alors BA=I (sans passer par Cayley-Hamilton. )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :