J'ai rencontré quelques difficultés dans 2-3 calculs de certains exercices; je connais les résultats mais je ne sais pas quels sont les intermédiaires pour y arriver. Pouvez vous m'aider? (en détaillant le maximum possible)
si vous pouviez m'aider avant lundi...
merci d'avance
en rouge les puissances
1) a et b sont des réels non nuls. Mettre sous forme bm/an où m et n appartiennent à |N.
(a²b)5/(-a³)4
(-ab²)(-ab)²/(-a) 7
2) Ecrire sous une seule puissance
(-x²)(-x)²/(x³)-²
3) Résoudre dans |R les équat° suivantes:
5x(x+1/3)² = 6x² +2x
(2x+3)² - (5x+7)² = 0
4) Soit n un entier relatif, écrire le plus simplement les réels suivants:
(-3)²n/3 -n-1
3n+²-3n
Calcul littéral (2de)
9 messages
- Page 1 sur 1
Mon dieu, Nesta! Ca faisait longtemps :++:
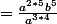 (a^b)^c = a^{b*c}, (-a)^k si k = 0 (2) = a^k.
(a^b)^c = a^{b*c}, (-a)^k si k = 0 (2) = a^k.

(-ab²)(-ab)²/(-a)^7
(a^2b^2)}{-a^7} = \frac{-a^3b^4}{-a^7}= \frac{b^4}{a^4}) sauf erreur.
sauf erreur.
(-x²)(-x)²/(x³)-²
}{x^{-6}} = \frac{-x^4}{\frac{1}{x^6}} = -x^{10})
(c'était bien (x^3)^-2 en bas?)
5x(x+1/3)² = 6x² +2x
^2 = 6x+2) Simplification par x, on retient que x=0 est solution...
Simplification par x, on retient que x=0 est solution...
 = 6x+2) et la ca devient plus simple
et la ca devient plus simple 
Nesta a écrit:(a²b)^5/(-a³)^4
(-ab²)(-ab)²/(-a)^7
(-x²)(-x)²/(x³)-²
(c'était bien (x^3)^-2 en bas?)
5x(x+1/3)² = 6x² +2x
Eh salut Anima! Ca fait pas mal de temps c'est vrai... :we:
Merci de ton aide!
C'est un des points que je n'ai pas trop compris... lorsque le nombre à mettre en puissance est négatif...pourquoi tu es passé de (-a³) à (a³)
Comment est ce que t'es passé de(a^2b^2)}{-a^7}) à
à 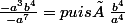 ? :mur:
? :mur:
Je n'arrive pas trop à finir..est ce qu'il faut passer le (6x+2) à gauche pour obtenir x²+2x/3+1/9=0 ou 6x+2=0 ?
Désolée...les vacances ont eu un effet néfaste sur moi :--:
Merci de ton aide!
anima a écrit:(-a)^k si k = 0 (2) = a^k.
C'est un des points que je n'ai pas trop compris... lorsque le nombre à mettre en puissance est négatif...pourquoi tu es passé de (-a³) à (a³)
anima a écrit:(-ab²)(-ab)²/(-a)^7sauf erreur.
Comment est ce que t'es passé de
anima a écrit:et la ca devient plus simple
Je n'arrive pas trop à finir..est ce qu'il faut passer le (6x+2) à gauche pour obtenir x²+2x/3+1/9=0 ou 6x+2=0 ?
Désolée...les vacances ont eu un effet néfaste sur moi :--:
Nesta a écrit:Eh salut Anima! Ca fait pas mal de temps c'est vrai... :we:
Merci de ton aide!
C'est un des points que je n'ai pas trop compris... lorsque le nombre à mettre en puissance est négatif...pourquoi tu es passé de (-a³) à (a³)
Ce n'était pas (-a^3) mais (-a^3)^4. 4 est pair, non? :briques:
Comment est ce que t'es passé deà
? :mur:
b^2 * b^2 = b^4
- reste -
a * a^2 = a^3
Apres, j'ai simplifié les facteurs -1, réduit les puissances, et voila...
Je n'arrive pas trop à finir..est ce qu'il faut passer le (6x+2) à gauche pour obtenir x²+2x/3+1/9=0 ou 6x+2=0 ?
Désolée...les vacances ont eu un effet néfaste sur moi :--:
Discriminant? :we:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
