Calcul avec dérivée partielle et seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 05 Fév 2014, 15:23
par Aktar » 05 Fév 2014, 15:23
Bonjour,
J'ai un peu de mal à trouvé la réponse au calcul suivant
J'ai Y = f(X) - X . f ' (X)
avec X = Z/a
et on en déduit que
dY/dZ = f ' (X) - X . f '' (X) . dX/dZ - f ' (X)
Je ne vois pas du tout comment obtenir cette dernière ligne de calcul...
Quelqu'un pourrait m'aider?.
Merci

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 05 Fév 2014, 15:34
par Ericovitchi » 05 Fév 2014, 15:34
Et bien par exemple tu écris :
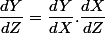
et tu dérives normalement par les formules habituelles , ça donne :
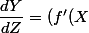-f '(X)-Xf"(X)).\dfrac{dX}{dZ}=-X.f"(X).\dfrac{dX}{dZ})
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 05 Fév 2014, 16:48
par Aktar » 05 Fév 2014, 16:48
ok super,
en gros je dérive F(x) et j'obtiens tout naturellement F'(X)... et la dérivée de -X f'(X) donne -X f''(X)... mais comment obtenir le deuxième F'(X)?
merci encore
-
Black Jack
 par Black Jack » 05 Fév 2014, 17:12
par Black Jack » 05 Fév 2014, 17:12
Aktar a écrit:ok super,
en gros je dérive F(x) et j'obtiens tout naturellement F'(X)... et la dérivée de -X f'(X) donne -X f''(X)... mais comment obtenir le deuxième F'(X)?
merci encore
Non, la dérivée (par rapport à X) de -X f'(X) donne - f'(X) - X.f''(X)
:zen:
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 05 Fév 2014, 17:27
par Aktar » 05 Fév 2014, 17:27
Black Jack a écrit:Non, la dérivée (par rapport à X) de -X f'(X) donne - f'(X) - X.f''(X)
:zen:
ah ok, pourrais tu m'expliquer stp?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 05 Fév 2014, 17:42
par Ericovitchi » 05 Fév 2014, 17:42
la dérivée d'un produit uv est u'v+v'u donc la dérivée de Xf '(X) est f '(X)+Xf"(X)
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 05 Fév 2014, 17:49
par Aktar » 05 Fév 2014, 17:49
Merci beaucoup c'est très claire.
Par contre dans ma correction j'ai
G= 1/f'(X)
et on me dis que
dG/dZ= [-f''(Y)/(f'(Y)² ] . dY/dZ
Je sais que la dérivée de 1/x = -1/x²... mais comment expliquer qu'il y es une dérivée seconde au numérateur?
Merci beaucoup pour votre aide préciseuse
-
Black Jack
 par Black Jack » 05 Fév 2014, 17:58
par Black Jack » 05 Fév 2014, 17:58
Si G(x) = u(x)/v(x)
G'(x) = (u'v-uv')/v²
Ici, on est dans un cas particulier où u(x) est une constante.
u(x) = 1 ---> u'(x) = 0
v(x) = f'(x) et donc v' = f''(x)
G'(x) = (u'v-uv')/v²
G'(x) = (0*f'(x) - 1*f''(x))/(f'(x))²
G'(x) = -f''(x)/(f'(x))²
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
