Besoin d'aide sur le calcul de racines carrées

[jalal]

Bonjour,
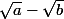
On me demande d'exprimer sous la forme ou et sont des rationnels.
Pouvez vous me donner une piste?
Merci.

[rene38]

Bonsoir


On élève au carré :

soit en développant

d'où on tire et
et sont alors les racines de l'équation du second degré

[yvelines78]

bonsoir,

même début :
a+b-2V(ab)=2-V3
d'où le système :
{a+b=2
{2V(ab)=V3
<--->
{a=2-b
{V(4ab)=V3
<--->
{a=2-b
{V(4ab)=V3
<--->
{a=2-b
{4ab=3
<--->
{a=2-b
{4(2-b)*b=3
<--->
{a=2-b
{-4b²+8b-3=0
delta=16
b=1/2 et a=3/2 ou b=3/2 et a=1/2

V(1/2)-V(3/2)=V(2-V3)
ou
V(3/2)-V(1/2)=V(2-V3)

[Nightmare]

Bonsoir

En deux lignes :

2-V(3)=3-V(3)-1=(V(3)-1)² (Identité remarquable)
Donc V(2-V(3))=|V(3)-1|=V(3)-1

:happy3:

[Chimomo]

Hmm, quelque peu curieux que V(1/2) - V(3/2) = V(3/2) - V(1/2) (ca veux dire que c'est aussi égal à 0) non ?

En fait ton raisonnement n'est pas un vrai raisonnement par équivalence parceque tu élève une églité au carré et ceci ne conserve pas l'équivalence (ca "rajoute" des solutions au sytème).

Donc il faut que tu regarde quel cas est vraiment juste et quel cas a été rajouté par le passage au carré pour ne pas écrire un résultat absurde.

[smaths]

Bonjour Jalal,

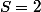
Prendre la réponse de Rene38, et poursuivre avec et , résoudre l'équation et penser qu'une racine carrée est toujours positive. Tu obtiendras l’unique solution recherchée.

Amitiés,
Soutiens Maths,
Ahmed.