Arithmétique terminal

par **kamena** » 17 Mar 2017, 16:14

bonjour !
j'ai besoin d'aide pour cet exercice.
voici l'énoncé :
Un nombre à quatre est un carré parfait. Le chiffre des unités est égal au chiffre des dizaines et le chiffre des centaines est égal au chiffre des unité de mille .
montrer que ce nombre est divisible par 121 .Trouver ce nombre.

par **Mimosa** » 17 Mar 2017, 16:40

Bonjour

Le nombre s'écrit

. L'énoncé dit que

et

. Essaye d'exploiter...

par **WillyCagnes** » 17 Mar 2017, 16:52

bjr

ton nombre s'écrit AACC= k x121
2299
3388
4477
5566
6655
7744
8833
te laisse deviner le suivant... :mrgreen:

et parmi ces nombres, il y a un carré parfait à trouver

par **kamena** » 17 Mar 2017, 17:05

excuse-moi! je ne comprends pas tellement.
si on désigné par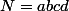

, comment exploiter les informations données.
donc N est l'ensemble des multiples de 121.

par **Mimosa** » 17 Mar 2017, 17:36

Ton nombre s'écrit donc

. Par conséquent,

doit être divisible par 11, et il doit être un carré.

par **kamena** » 17 Mar 2017, 17:47

merci beaucoup pour vos réponses.comme

ie N est divisible par 11.
comment trouver alors N ? suffit de dire que N est l'ensemble des multiples de11?
merci d'avance !

par **WillyCagnes** » 17 Mar 2017, 18:03

avec (100A+C)=11K
le hasard fait bien les choses : A+C=11
A=7
C=4

N= 88² = 7744=11²x8²= 121 x 64

par **kamena** » 17 Mar 2017, 21:54

merci pour votre intervention!
comme vous l'avez souligné "le hasard fait bien les choses "
permettez-moi de dire c'est du hasards mais de l'évidence......
merci cordialement à plus

Arithmétique terminal

arithmétique terminal

Re: arithmétique terminal

Re: arithmétique terminal

Re: arithmétique terminal

Re: arithmétique terminal

Re: arithmétique terminal

Re: arithmétique terminal

Re: arithmétique terminal

Qui est en ligne