Argument en nombre comlexes.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 15:53
par Accordiola1 » 27 Fév 2007, 15:53
Bonjour.
Voila, dans un DM sur les complexes, j'en suit arrivé ici :
cos ° = (Cos pi/6) / 3
sin ° = (Sin pi/6) / 3
Et j'arrive pas à trouver téta ( ° )
Merci d'avance :) :stupid_in
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 16:16
par amine801 » 27 Fév 2007, 16:16
slt
ta question n'est pas claire tu peux poser la question que tu avait a l'origine
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 16:20
par Accordiola1 » 27 Fév 2007, 16:20
Désolé, en fait j'ai une question ou on me demande de calculer le module et un argument du nombre complexe.
Pour le module c'est fait, et j'ai commencé l'argument, c'est ce que je vous donne.
Et je n'arrive pas à finir cette question, ou il faut que je trouve téta (ce que j'ai symbolisé ° ) à partir des deux équations citée précédemment.
Merci :happy2:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 16:27
par amine801 » 27 Fév 2007, 16:27
c'est quoi le nombre complexe dont l'argument est demande peut-tu
le donner
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 16:30
par Accordiola1 » 27 Fév 2007, 16:30
Alors le voici :
z2 = 3cos(pi/6) - 3sin(pi/6)i
Merci d'avance pour ton aide. :id:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 16:41
par amine801 » 27 Fév 2007, 16:41
quand z=a+bi alors
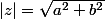
donc
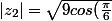^2+9sin(\frac{\pi}{6})^2}=3)
ainsi
-sin(\frac{\pi}{6})))
vu que cos(-x)=cos(x) et sin(-x)=-sin(x)
alors
+sin(-\frac{\pi}{6})))
alors
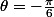
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 16:48
par Accordiola1 » 27 Fév 2007, 16:48
d'accord, merci beaucoup amine.
On ce comprenait pas parceque je cherchais pas à utiliser cette méthode pour l'argument mais :
cos ° = a / |Z|
sin ° = b / |z|
Mais j'ai comprit ta méthode donc no soucis.
Merci
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 17:02
par amine801 » 27 Fév 2007, 17:02
justement tu avait une petite erreure en divisant deux fois par |z|
cos ° = (Cos pi/6)
sin ° = (Sin pi/6)
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 17:06
par Accordiola1 » 27 Fév 2007, 17:06
Oui, je vient m'en apercevoir, j'avais oublié de multiplier par 3 le nominateur :marteau:
Donc pour z3 = -3cos(pi/6) - 3sin(pi/6)i
je trouve toujours un module de 3 et en revanche, un argument de + pi/6 ?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 17:11
par amine801 » 27 Fév 2007, 17:11
pour le module c'est bon sinom pour

c'est faux
la forme d'un nombre complexe c'est
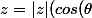+sin(\theta)i))
et pas
-sin(\theta)i))
faux
utilise le fait que
=-cos(x))
=-sin(x))
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 17:22
par Accordiola1 » 27 Fév 2007, 17:22
amine801 a écrit:la forme d'un nombre complexe c'est
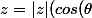+sin(\theta)i))
et pas
-sin(\theta)i))
faux
Je ne comprend plus la, comment tu trouve ces formules par rapport à mon éxos ?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 17:32
par amine801 » 27 Fév 2007, 17:32
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 17:43
par Accordiola1 » 27 Fév 2007, 17:43
ah vi, ta méthode est beaucoup plus simple que la mienne.
donc la solution est

Ensuite (les exponentielles ce rajoutes :hum: )
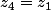

avec z1 = 3(cos

/6 + i sin

/6)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 17:48
par amine801 » 27 Fév 2007, 17:48
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 18:40
par Accordiola1 » 27 Fév 2007, 18:40
Merci

Ensuite (les exponentielles se rajoutent :hum: )
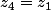

EDIT : Correction : 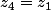

avec z1 = 3(cos

/6 + i sin

/6)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 19:51
par amine801 » 27 Fév 2007, 19:51
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 21:27
par Accordiola1 » 27 Fév 2007, 21:27
Accordiola1 a écrit:Ensuite (les exponentielles ce rajoutes :hum: )
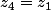

avec z1 = 3(cos

/6 + i sin

/6)
Zut, ça va vraiment pas moi ce soir...
C'est
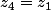

Et donc je trouve
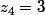

Ce qui est juste (on me l'indique dans l'énoncé).
donc

et
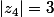
?
Et la question qui suit : quelle est la forme algébrique ?
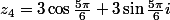
?
Merci :we:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 21:36
par amine801 » 27 Fév 2007, 21:36
oui c'est bien ca la forme algebrique
ps:j'ai modifie le message precedant
-
Accordiola1
- Membre Naturel
- Messages: 46
- Enregistré le: 27 Fév 2007, 11:00
-
 par Accordiola1 » 27 Fév 2007, 21:40
par Accordiola1 » 27 Fév 2007, 21:40
D'accord merci, on verra la suite demain :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
