bonsoir
je vous serez reconnaissante si vous pouviez m expliquer l arccos merci bcp d avance
Arccos
3 messages
- Page 1 sur 1
Bonjour
La fonction arcos est la fonction qui répond à la question : si x est un nombre réel, quel angle a x comme cosinus ?
Bien évidemment, il n'y a pas toujours de réponse à cette question, puisque aucun angle n'a 2 comme cosinus. Ainsi, la fonction arcos a pour ensemble de définition [-1 ; 1].
D'autre part, étant donné un réel, plusieurs angles ont ce réel pour cosinus. Ainsi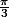 et
et 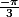 ont tous les deux pour cosinus
ont tous les deux pour cosinus 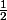 , ainsi d'ailleurs que
, ainsi d'ailleurs que 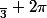
On convient de choisir comme arcos l'angle compris entre 0 et .
.
Ainsi seul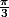 est l'arcos de
est l'arcos de 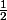
C'est comme pour la racine carrée : les deux nombres -2 et 2 ont pour carré 4, on convient que seul 2 est la racine carrée de 4.
La fonction arcos est la fonction qui répond à la question : si x est un nombre réel, quel angle a x comme cosinus ?
Bien évidemment, il n'y a pas toujours de réponse à cette question, puisque aucun angle n'a 2 comme cosinus. Ainsi, la fonction arcos a pour ensemble de définition [-1 ; 1].
D'autre part, étant donné un réel, plusieurs angles ont ce réel pour cosinus. Ainsi
On convient de choisir comme arcos l'angle compris entre 0 et
Ainsi seul
C'est comme pour la racine carrée : les deux nombres -2 et 2 ont pour carré 4, on convient que seul 2 est la racine carrée de 4.
merci de votre aide a écrit:bonsoir
je vous serez reconnaissante si vous pouviez m expliquer l arccos merci bcp d avance
L'équation cos(x)=a a une infinité de solutions si elle en a une. En effet s'il existe x0 tel que
Finalement l'ensemble des solutions est l'ensemble des x que l'on peut écrire :
Or il est souvent pratique, lorsque l'on a un nombre a qui est le cosinus d'un certain angle, de désigner par une expression l'un des multiples angles qui ont a pour cosinus. On sait que dans un intervalle de largeur
Il résulte de cette définition que cos(Arcos(a)) = a (si -1<=a<=1, bien sûr)
Par contre Arccos(cos(x)) peut être différent de x. Par exemple si
Cela éclaire-t-il ta lanterne ?
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
