Bonjour, pour mon Grand Oral, je cherche à répondre à la question suivante :
Peut-on donner une approximation d'un nombre irrationnel à l'aide de suites ?
Je vais d'abord parler de la suite de Fibonacci et du nombre d'or et je cherchais s'il existait d'autres nombres irrationnels que l'on puisse approximer par une suite définie par récurrence. J'ai trouvé sur math-forum des façons d'approximer pi mais soit c'était des suites où il fallait faire chaque terme manuellement soit pi était lui-même compris dans la relation de récurrence.
Connaissez-vous des suites par récurrence (un peu comme celle de Fibonacci) qui permettent de faire une approximation d'un nombre irrationnel plus les termes sont grand ?
Approximer un nombre irrationel à l'aide de suites(Grand ora
5 messages
- Page 1 sur 1
Re: Approximer un nombre irrationel à l'aide de suites(Grand
Pour tous les nombres "racine carrée de", on a la suite de Héron :
)
Qui converge vers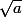 (le point fixe de la fonction qui définit la relation de récurrence)
(le point fixe de la fonction qui définit la relation de récurrence)
Qui converge vers
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Approximer un nombre irrationel à l'aide de suites(Grand
bonjour,
soit a >0 , la suite définie par
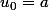
)
a pour limite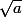
Cette suite est définie par la méthode de Newton appliquée à la fonction f:
=x^2-a)
soit a >0 , la suite définie par
a pour limite
Cette suite est définie par la méthode de Newton appliquée à la fonction f:
Re: Approximer un nombre irrationel à l'aide de suites(Grand
Merci beaucoup pour vos réponses sur la suite de Héron ça va beaucoup m'aider !
Re: Approximer un nombre irrationel à l'aide de suites(Grand
N'importe quel nombre peut être approché par une suite de rationnels, sauf peut-être des exemples totalement atypiques... mais je n'en vois pas.
Par exemple, on cherche le nombre x tel que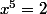
On sait qu'il y a une solution, entre 1 et 2. Et il n'y en a qu'une.
On commence avec x=1 , on calcule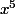 , trop petit.
, trop petit.
On ajoute 1/2 , on calcule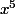 , trop grand.
, trop grand.
On enlève 1/4 , on calcule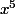 , trop grand
, trop grand
etc etc, à chaque fois, on ajoute ou enlève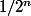
Au bout de 10 étapes, on enlève ou on retire 1/1024, on a donc une réponse qui est correcte, avec une incertitude inférieure à 1/1024
Accessoirement, cette méthode s'appelle la dichotomie. C'est un mot qui peut te servir.
Pareil pour des équations plus tordues :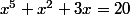 par exemple,
par exemple,
Par exemple, on cherche le nombre x tel que
On sait qu'il y a une solution, entre 1 et 2. Et il n'y en a qu'une.
On commence avec x=1 , on calcule
On ajoute 1/2 , on calcule
On enlève 1/4 , on calcule
etc etc, à chaque fois, on ajoute ou enlève
Au bout de 10 étapes, on enlève ou on retire 1/1024, on a donc une réponse qui est correcte, avec une incertitude inférieure à 1/1024
Accessoirement, cette méthode s'appelle la dichotomie. C'est un mot qui peut te servir.
Pareil pour des équations plus tordues :
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
