Bonjour a tous ! J'aurai besoin de votre aide pour résoudre un exercice que je ne comprends pas:
En connaissant les coordonnées de deux points A et B , écrire un algorithme ( en language naturel ) qui renvoie les coordonnées de deux points C et D tels que ABCD soit un carré .
On expérimentera d'abord avec Géogébra por découvrir les relations entre les coordonnées des points
Je vous remercie de votre aide !
Algorithme
8 messages
- Page 1 sur 1
Bonjour,
par définition un carré possède des côtés égaux deux à deux et 4 angles perpendiculaires.
Voici les étapes auxquels réfléchir avant de se lancer dans l'algorithme.
1) Comment connaître la distance d'un segment à partir des coordonnées de A et B
2) Comment placer un point C tel que ABC soit perpendiculaire et que BC = AB
3) Idem pour D
Essaye de répondre à ses questions ici et on pourra poursuivre vers l'algorithme
par définition un carré possède des côtés égaux deux à deux et 4 angles perpendiculaires.
Voici les étapes auxquels réfléchir avant de se lancer dans l'algorithme.
1) Comment connaître la distance d'un segment à partir des coordonnées de A et B
2) Comment placer un point C tel que ABC soit perpendiculaire et que BC = AB
3) Idem pour D
Essaye de répondre à ses questions ici et on pourra poursuivre vers l'algorithme
ampholyte a écrit:Bonjour,
par définition un carré possède des côtés égaux deux à deux et 4 angles perpendiculaires.
Voici les étapes auxquels réfléchir avant de se lancer dans l'algorithme.
1) Comment connaître la distance d'un segment à partir des coordonnées de A et B
2) Comment placer un point C tel que ABC soit perpendiculaire et que BC = AB
3) Idem pour D
Essaye de répondre à ses questions ici et on pourra poursuivre vers l'algorithme
Je ne comprends pas bien .. Mais j'ai oubliée de préciser a=(3;2) B=(9;1) c=(10;7) D=(4;8)
Excusez moi mais mon niveau de math est plutôt médiocre ..
re
laitha a écrit:Je ne comprends pas bien .. Mais j'ai oubliée de préciser a=(3;2) B=(9;1) c=(10;7) D=(4;8)
Excusez moi mais mon niveau de math est plutôt médiocre ..
SVP merci de m'aider a résoudre ce probléme
ampholyte a écrit:Je ne comprends pas vraiment votre problème. Serait-il possible d'avoir l'exercice en entier ?
Je vous ai donner l'énoncé en entier .. Il faut " écrire un algorithme (en language naturel) qui renvoie les coordonnées de deux points C et D tels que ABCD soit un carré " Je ne comprends pas .. Je pense qu'il faut s'aider des coordonnées non ?
Oui tout à fait d'où mes questions pour toi.
1) Comment connaître la distance d'un segment à partir des coordonnées de A et B ?
Réponse : Il y a une formule qui permet à partir des coordonnées de trouver la distance entre A et B :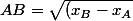^2 + (y_B - y_A)^2})
2) Comment placer un point C tel que ABC soit perpendiculaire et que BC = AB
la formule :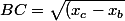^2 + (y_c - y_b)^2} = AB) est toujours valable.
est toujours valable.
Tu peux également dire que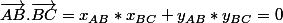 par définition du produit scalaire.
par définition du produit scalaire.
Il y a d'autres solutions encore...
1) Comment connaître la distance d'un segment à partir des coordonnées de A et B ?
Réponse : Il y a une formule qui permet à partir des coordonnées de trouver la distance entre A et B :
2) Comment placer un point C tel que ABC soit perpendiculaire et que BC = AB
la formule :
Tu peux également dire que
Il y a d'autres solutions encore...
laitha a écrit:Bonjour a tous ! J'aurai besoin de votre aide pour résoudre un exercice que je ne comprends pas:
En connaissant les coordonnées de deux points A et B , écrire un algorithme ( en language naturel ) qui renvoie les coordonnées de deux points C et D tels que ABCD soit un carré .
On expérimentera d'abord avec Géogébra por découvrir les relations entre les coordonnées des points
Je vous remercie de votre aide !
Bonjour
Si tu as vu les nombres complexes et les similitudes, tu peux avoir facilement les formules qui donnent les coordonnées de C et de D en fonctions des coordonnées de A et de B.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 127 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
