Bonjour à tous,
Voilà mon problème, je dois compléter un algorithme mais je ne comprends pas vraiment comment faire.
On considère la suite Sn= somme de k x (n-k) pour k allant de 1 à n.
Je dois compléter cet algorithme pour qu'il affiche le nième terme de la suite.
Saisir n
S prend la valeur ....
Pour k de 1 à ... Faire
S prend la valeur...
Fin pour
Afficher S
Pourriez-vous m'expliquer comment je peux faire ? Merci d'avance à tous !
Algorithme
4 messages
- Page 1 sur 1
Raiponce a écrit:Bonjour à tous,
Voilà mon problème, je dois compléter un algorithme mais je ne comprends pas vraiment comment faire.
On considère la suite Sn= somme de k x (n-k) pour k allant de 1 à n.
Je dois compléter cet algorithme pour qu'il affiche le nième terme de la suite.
Saisir n
S prend la valeur ....
Pour k de 1 à ... Faire
S prend la valeur...
Fin pour
Afficher S
Pourriez-vous m'expliquer comment je peux faire ? Merci d'avance à tous !
Bonjour,
Tu as le bon raisonnement.
On décompose en plusieurs étapes :
- On demande la valeur de n à l'utilisateur et on initialise S à 0
- On effectue une boucle de 1 à n et on calcule S = S + (ité * (n - ité)) avec ité la valeur d'itération
- Fin de boucle
- On affiche S
En C ça pourrait donner :
- Code: Tout sélectionner
int n = 0
int s = 0
int i = 0
printf("saisir une valeur pour n");
scanf("%d",&n);
for(i = 1 ; i < n ; i++){
s = s + i*(n-i);
}
printf("valeur de s : %d", s);
Il faut donc compléter l'algorithme suivant
afin de calculer pour une valeur donnée la valeur de
donnée la valeur de 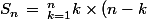)
Comme on peut le constater, l'algorithme est déjà fort complet et il ne reste plus qu'à remplacer les points de suspension (...) par l'objet adéquat.
Etudions la structure de cet algorithme:
-*- Il commence par SAISIR N et termine par AFFICHER S: c'est assez simple, on doit fournir à la machine la valeur de et elle doit calculer la valeur
et elle doit calculer la valeur  .
.
Il apprend donc que dans cet algorithme, la variable N contient la valeur n du rang de la suite et à la fin de celui-ci la variable S doit contenir .
.
-**- Il y a deux fois l'opération S PREND_LA_VALEUR ... . Tiens!Tiens! C'est bizarre.
Cela prouve que la valeur finale de n'est pas calculer en une seule fois, mais qu'elle est construite au fur et à mesure du déroulement de cet algorithme.
n'est pas calculer en une seule fois, mais qu'elle est construite au fur et à mesure du déroulement de cet algorithme.
-***- Il y a au coeur de cet algorithme une boucle POUR K DE 1 A ...
Voilà c'est cette boucle qui doit permettre de construire au fur et à mesure dans la variable S la valeur finale attendue, c'est à dire .
.
Voilà ces trois observations permettent de bien cerner l'algorithme. La question qu'il faut se poser; est-ce qu'utiliser une boucle pour construire la valeur finale de dans une variable unique S est une bonne idée ?
dans une variable unique S est une bonne idée ?
A priori oui.
Car est une somme. On peut calculer cette somme pas à pas en la décomposant. C'est ce que doit faire cet algorithme. On part d'une valeur initale dans S et à chaque fois que l'on effectue la boucle on ajoute un terme de la somme.
est une somme. On peut calculer cette somme pas à pas en la décomposant. C'est ce que doit faire cet algorithme. On part d'une valeur initale dans S et à chaque fois que l'on effectue la boucle on ajoute un terme de la somme.
La définition mathématique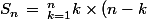) donne justement l'expression générale des termes de la somme.
donne justement l'expression générale des termes de la somme.
En plus, il est clair qu'il y a une similitude entre le k noté dans l'expression mathématique et la variable K de l'algorithme.
Comme le suggère ptitnoir, faire quelques essais pour décomoser la somme S_n avec les valeurs de n = 1,2, 3 ou 4 permet de bien se rendre compte du déroulement des calculs et de la façon dont les termes de la somme s'ajoutent.
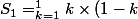\,=\,1\times(1-1) = 1\times0 = 0 \\<br />S_2 = \bigsum_{k=1}^{2} k \times (2-k)\,=\,1\times(2-1)\,+\,2\times(2-2)= 1\times1 + 2\times0 = 1+0 = 1\\<br />S_3 = \bigsum_{k=1}^{3} k \times (3-k)\,=\,1\times(3-1)\,+\,2\times(3-2)\,+\,3\times(3-3)= 1\times2 +2\times1+ 3\times0 = 2 + 2 + 0 = 4\\<br />S_4 = ....)
- Code: Tout sélectionner
SAISIR N
S PREND_LA_VALEUR ....
POUR K DE 1 A ... FAIRE
: S PREND_LA_VALEUR ....
FIN POUR
AFFICHER S
afin de calculer pour une valeur
Comme on peut le constater, l'algorithme est déjà fort complet et il ne reste plus qu'à remplacer les points de suspension (...) par l'objet adéquat.
Etudions la structure de cet algorithme:
-*- Il commence par SAISIR N et termine par AFFICHER S: c'est assez simple, on doit fournir à la machine la valeur de
Il apprend donc que dans cet algorithme, la variable N contient la valeur n du rang de la suite et à la fin de celui-ci la variable S doit contenir
-**- Il y a deux fois l'opération S PREND_LA_VALEUR ... . Tiens!Tiens! C'est bizarre.
Cela prouve que la valeur finale de
-***- Il y a au coeur de cet algorithme une boucle POUR K DE 1 A ...
Voilà c'est cette boucle qui doit permettre de construire au fur et à mesure dans la variable S la valeur finale attendue, c'est à dire
Voilà ces trois observations permettent de bien cerner l'algorithme. La question qu'il faut se poser; est-ce qu'utiliser une boucle pour construire la valeur finale de
A priori oui.
Car
La définition mathématique
En plus, il est clair qu'il y a une similitude entre le k noté dans l'expression mathématique et la variable K de l'algorithme.
Comme le suggère ptitnoir, faire quelques essais pour décomoser la somme S_n avec les valeurs de n = 1,2, 3 ou 4 permet de bien se rendre compte du déroulement des calculs et de la façon dont les termes de la somme s'ajoutent.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 150 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
