Algorithme probabilité

[Mama27]

Bonjour à tous,

Je souhaiterai un peu d'aide svp pour mon dm de TS.
Cet exercice est sur un algorithme mais l'année précédente je n'ai vraiment appris programmer donc je suis un peu coincée.

Voilà l'exercice :

La roue d'une loterie est divisée en 5 secteurs identiques numérotés de 1 à 5 . On fait tourner la roue n fois ( n nombre entier naturel, (n》1)). La variable aléatoire X donne le rang de la première apparition du numéro 5 et X donne la valeur 0 si le 5 n'est pas sorti.

1. On simule cette expérience aléatoire avec l'algorithme suivant :
X <--- nombre aléatoire de 1 à 5.
J <--- 1.
Tant que : ... et ...
X <--- nombre entier aléatoire de 1 à 5.
J <--- J+1.
Fin Tant que.
Si J 《 n alors
Afficher ...
Sinon
Afficher ...
Fin Si.

a. Recopier et compléter cet algorithme.
b. Coder cet algo. dans un langage de programmation (calculatrice ou autre) et exécuter plusieurs fois le programme obtenu.

2. a. Déterminer la loi de proba. de la variable X. On dit que cette loi géométrique troquée de paramètres n et p = 1/5.
b. Vérifier que :
P(X=1)+P(X=2)+...+P(X=n)+P(X=0)=1.
c. Sur l'écran de calcul formel ci-dessus, on détermine E(X) pour n=30

1| Somme[k*0.8^(k-1)*0.2,k,1,30]
|~4.96
Justifier la formule utiliséen

d. Calculer E(X) pour de grandes valeurs de n. Que remarque-t-on?
Interpréter ce résultat.

Je vous remercie d'avance pour votre aide.

[aviateur]

Bonjour

Il faut comprendre d'abord l'algorithme (même s'il y a des trous)
On joue un certain nombre de fois (tant que) mais il faudra bien s'arrêter:
2 cas se présentent le 5 va sortir avant le nième coup ou ne sortira pas avant le n_ième coup.
donc cela sera
Tant que X<5 et j <n.
Mais attention il manque la déclaration de n au début de l'algorithme

Pour afficher c'est facile à deviner.

[Mama27]

Merci de m'aider
D'accord j'ai compris l'algorithme sauf le j pourquoi était-il là je n'ai pas bien compris à quoi il sert.

[pascal16]

Je pense qu'on essaie de te faire dire qu'on tend quand n est grand vers une loi exp (ou une géo non tronquée) avec une espérance de 1/p soit 1/(1/5) = 5.

Si ton prof a l'habitude de faire des retours à la réalité, c'est cette valeur qui va servir au calcul du seuil de rentabilité de la loterie.

[aviateur]

Pour compléter la remarque de Pascal il y deux étapes dans ton problème
Tu fais une expérience aléatoire qui dépend d'un nombre n.
Il y a d'abord une partie expérimentale c'est la programmation.
C'est à dire que tu va simuler l'expérience autant de fois que tu veux avec différentes valeurs de n.

Et puis il y a la partie théorique où tu dois calculer la loi de X (en fonction d'un n fixé) . Qaund tu as calculer cette loi , tu dois aussi calculer l'espérance de X.
En principe tu trouveras et on remarque que E(X) tend vers 5 quand n tend vers l'infini. Résultat que l'on peut peut être deviner intuitivement sans calcul.
Mais le but de l'algorithme c'est de prendre n grand (on te propose n=30 mais tu peux changer)
et utilisant ton algorithme (qu'il faut prolonger) un certain nombre de fois (100 fois par exemple), tu feras la moyenne et tu trouveras quelque chose proche du résultat théorique et donc de 5 si n est grand.

[Mama27]

Oui mais pour la question 2 le n n'est pas donné donc comment faut il faire?
Est ce que le succès =(4/5)^n
Et l'échec = (4/5)^n*1/5 ?

[aviateur]

Pour la question 2. il faut faire le calcul pour un n qcq.

D'ailleurs pour commencer tu ne t'occupes pas de la valeur de n. En effet tu imagines que et tu détermine la loi de la v.a Y qui correspond à la première fois que le 5 sort.
Il faut donc calculer
Mais pour cela il est plus commode de calculer
(par convention poser q-0=0)

En effet
dc tu a une relation de récurrence

C'est une suite arithmetico-géométrique et tu peux alors calculer
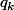en fonction de k.
Puis
(vérifier que

Maintenant pour X c'est facile
P(X=k)=P(Y=k) ,k=1,.....,n et P(X=0) et alors facile à trouver.

Pour l'espérance il faut appliquer la formule et j'ai déjà donné le résultat.

[Mama27]

Je vous remercie vraiment de m aider mais je ne comprend absolument rien, pourquoi n n'est pas définit ?

[aviateur]

C'est pas ça. n étant un nombre arbitraire fixé à l'avance (par exempel n=30) Le jeu c'est quoi on joue et on s'arrête dès que le 5 est sorti avant n coup où alors si au bout de n coup le 5 n'est pas sorti alors le jeu s'arrête.

Prenons 2 exemples n= 30 et n=40.
Dans les 2 cas P(X=1) ,P(X=2)..... P(X=30) c'est la même chose. Là où ça change dans le premier cas X=31 n'a pas lieu mais dans le deuxième oui.
Mais quand k<=n on a P(X=k)=P(Y=k). Ce qui change c'est que P(X=0)=1-(P(X=1)+P(X=2)+...P(X=n)).